POINT
- 三角関数の公式のほとんどは,単位円やグラフを描けば導ける.
- 例外的に「加法定理(3つ)」だけは暗記が必要.他の公式は加法定理から簡単に計算できる.
三角関数はあらゆる分野で現れます.ベクトルなどと同様に,ツールとしての役割が大きいです.小学校の算数で言えば「九九」のようなものだと言えるでしょう.但し,「九九」のように丸暗記するのではなく,幾何学的な意味を理解しながら,スラスラと計算できるようになることが重要です.
さらに,オイラーの公式を通して複素指数関数とも深い関係があります.
【関連記事】
定義
三角関数は「直角三角形の辺の比」で定義されます(下図).「辺の比」は相似な三角形で等しくなるため,三角関数の値は図の角度$\theta$だけで決まることがわかります.
座標軸上で負の領域にある辺については、長さもマイナスとして考えることに注意しましょう(下図).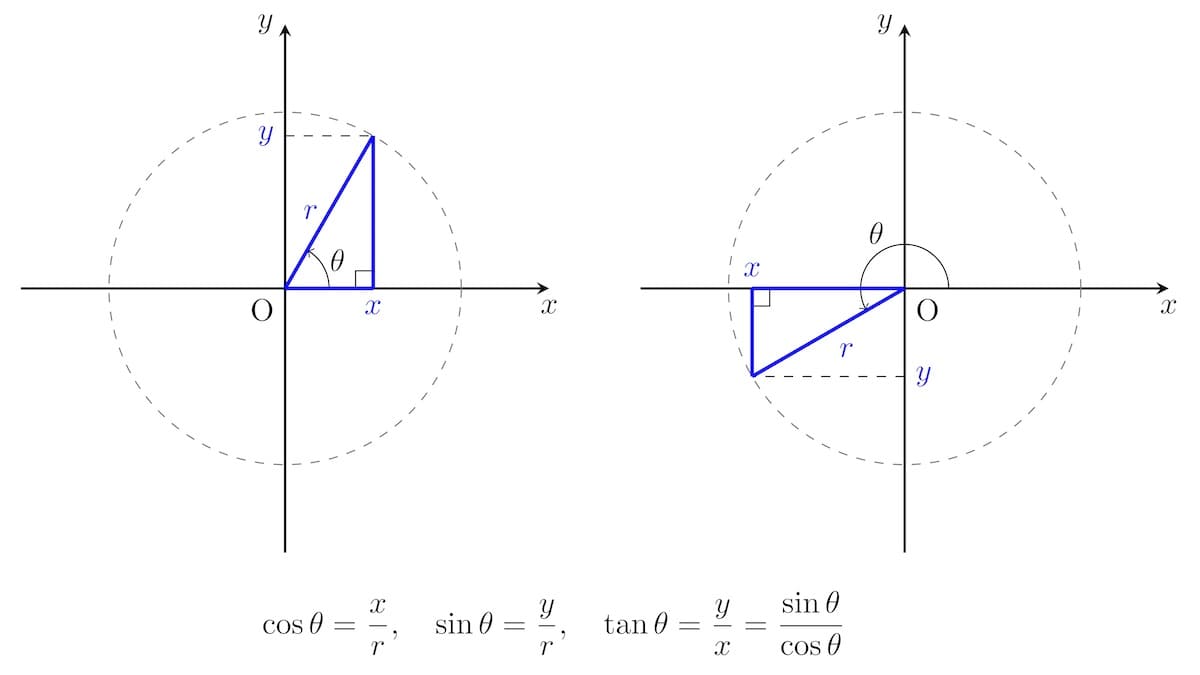
実用上は,単位円($r=1$の円)を描いて考えるとわかりやすいです.

単位円をもとにすれば,三角関数($\cos\theta$, $\sin\theta$, $\tan\theta$)のグラフを描くことができます: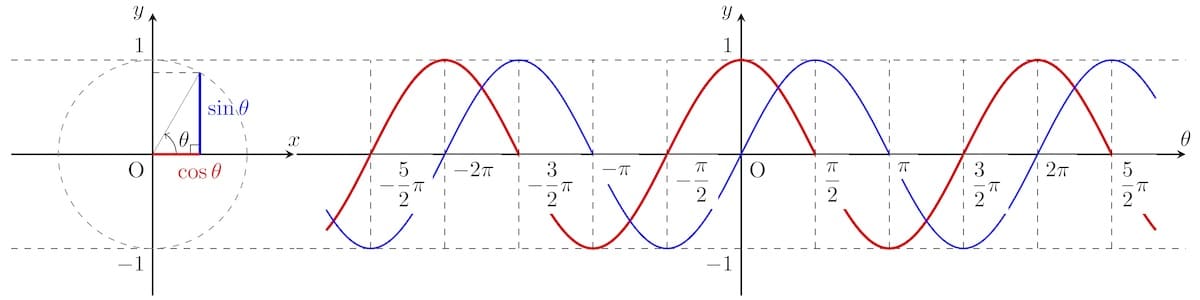
※$\tan\theta$のグラフは作成中...
性質
三角関数の性質をまとめてみます.暗記するのではなく,その都度「単位円やグラフ」を描いて導出する癖をつけましょう.単位円を描くことでわかる性質
- $\sin^2\theta+\cos^2\theta = 1$
- 直角三角形に対する「ピタゴラスの定理」からわかる.
- $\tan\theta=\dfrac{\sin\theta}{\cos\theta}$
- $\tan\theta$の定義そのもの.
- $n$を整数とするとき,$\cos(\theta + 2n\pi)=\cos\theta$,$\sin(\theta + 2n\pi)=\sin\theta$,$\tan(\theta + 2n\pi)=\tan\theta$ :
- $2\pi$ごとに同じ三角形が現れることからわかる.
グラフを描くことでわかる性質
- $\cos(\theta-\pi/2)=\sin\theta$
- 「$\sin\theta$のグラフ」=「$\cos\theta$を$\pi/2$だけ平行移動したグラフ」になっている(後で紹介する「加法定理」から導くこともできる).
覚えるべき公式
「加法定理」だけ覚えておけば,他の公式は簡単な計算により導出することができます.加法定理
以下の公式だけは,「九九」のように暗記してください.加法定理
\begin{aligned}
\sin(\alpha + \beta)
&=\sin\alpha\,\cos\beta + \cos\alpha\,\sin\beta \\
\cos(\alpha + \beta)
&=\cos\alpha\,\cos\beta - \sin\alpha\,\sin\beta \\
\tan(\alpha + \beta)
&=\frac{\tan\alpha + \tan\beta}{1-\tan\alpha\,\tan\beta}
\end{aligned}
\sin(\alpha + \beta)
&=\sin\alpha\,\cos\beta + \cos\alpha\,\sin\beta \\
\cos(\alpha + \beta)
&=\cos\alpha\,\cos\beta - \sin\alpha\,\sin\beta \\
\tan(\alpha + \beta)
&=\frac{\tan\alpha + \tan\beta}{1-\tan\alpha\,\tan\beta}
\end{aligned}
もし忘れてしまったら...
オイラーの公式:$e^{i\theta}=\cos\theta + i\sin\theta$から導くのが簡単です:
\begin{aligned}
&\textcolor{red}{\cos (\alpha + \beta)} + i\textcolor{blue}{\sin (\alpha + \beta)} \\
&=e^{i(\alpha + \beta)} \\
&=e^{i\alpha}e^{i\beta} \\
&=( \cos\alpha + i\sin\alpha)( \cos\beta + i\sin\beta) \\
&=(\textcolor{red}{\cos\alpha\,\cos\beta - \sin\alpha\,\sin\beta}) \\
&\quad+i(\textcolor{blue}{\sin\alpha\,\cos\beta + \cos\alpha\,\sin\beta} )
\end{aligned}
なので,実部・虚部を比較することにより$\sin(\alpha + \beta)$, $\cos(\alpha + \beta)$に関する公式が導けます.&\textcolor{red}{\cos (\alpha + \beta)} + i\textcolor{blue}{\sin (\alpha + \beta)} \\
&=e^{i(\alpha + \beta)} \\
&=e^{i\alpha}e^{i\beta} \\
&=( \cos\alpha + i\sin\alpha)( \cos\beta + i\sin\beta) \\
&=(\textcolor{red}{\cos\alpha\,\cos\beta - \sin\alpha\,\sin\beta}) \\
&\quad+i(\textcolor{blue}{\sin\alpha\,\cos\beta + \cos\alpha\,\sin\beta} )
\end{aligned}
$\tan(\alpha + \beta)=\dfrac{\sin(\alpha + \beta)}{\cos(\alpha + \beta)}$の公式は,「$\sin(\alpha + \beta)$と$\cos(\alpha + \beta)$の公式を$\tan$を出すように式変形」した
\begin{aligned}
\sin(\alpha + \beta)
&=\frac{1}{\cos\alpha\,\cos\beta}(\tan\alpha+\tan\beta)\\
\cos(\alpha + \beta)
&=\frac{1}{\cos\alpha\,\cos\beta}(1 - \tan\alpha\,\tan\beta )
\end{aligned}
から導けます.\sin(\alpha + \beta)
&=\frac{1}{\cos\alpha\,\cos\beta}(\tan\alpha+\tan\beta)\\
\cos(\alpha + \beta)
&=\frac{1}{\cos\alpha\,\cos\beta}(1 - \tan\alpha\,\tan\beta )
\end{aligned}
導ける公式
以下の公式は,使うたびに導出できるようにしておきましょう.加法定理の派生公式
上の加法定理で$\beta=-\alpha$とすれば,- $\sin(\alpha - \beta) = \sin\alpha\,\cos\beta - \cos\alpha\,\sin\beta $
- $\cos(\alpha - \beta) = \cos\alpha\,\cos\beta + \sin\alpha\,\sin\beta$
- $\tan(\alpha - \beta) = \dfrac{\tan\alpha - \tan\beta}{1 + \tan\alpha\,\tan\beta}$
2倍角の公式
$\alpha=\beta=\theta$とすれば「2倍角」の公式になる:- $\sin 2\theta=2\sin\theta \cos\theta$
- $\cos 2\theta=\cos^2\theta-\sin^2\theta =\begin{cases} \, 1 - 2\sin^2\theta\\ \, 2\cos^2\theta - 1 \end{cases}$
- $\tan 2\theta = \dfrac{2\tan\theta}{1 - \tan^2\theta}$
半角の公式
2倍角の公式($\cos 2\theta$)から「半角」の公式が導ける(以下で$\theta\rightarrow \theta/2$としたものが公式として紹介されることが多いですが,このままでも応用上問題ありません):- $\sin^2 \theta = \dfrac{1-\cos 2\theta}{2}$
- $\cos^2 \theta = \dfrac{1+\cos 2\theta}{2}$
- 上の2つから,$\tan^2 \theta = \dfrac{\sin^2 \theta}{\cos^2 \theta }=\dfrac{1-\cos 2\theta}{1+\cos 2\theta}$
積和の公式
$\sin(\alpha \pm \beta)$,$\cos(\alpha \pm \beta)$を適当に足し引きすることで,「三角関数の積を和に変換する」ことができます:- $\sin\alpha\,\cos\beta \,$$=\frac{1}{2} \bigl[ \sin(\alpha + \beta) + \sin(\alpha - \beta) \bigr]$
- $\cos\alpha\,\cos\beta $$=\frac{1}{2} \bigl[ \cos(\alpha + \beta) + \cos(\alpha - \beta) \bigr]$
- $\sin\alpha\,\sin\beta \,$$=\frac{1}{2} \bigl[ -\cos(\alpha + \beta) + \cos(\alpha - \beta) \bigr]$
和積の公式
同じように,「三角関数の和を積に変換する」公式は\begin{aligned}
&\sin(\alpha + \beta) \pm \sin(\alpha - \beta) \\
&=
\begin{cases}
\, 2\sin\alpha\,\cos\beta &(+\text{の場合})\\
\, 2\cos\alpha\,\sin\beta &(-\text{の場合})
\end{cases}
\end{aligned}
と,&\sin(\alpha + \beta) \pm \sin(\alpha - \beta) \\
&=
\begin{cases}
\, 2\sin\alpha\,\cos\beta &(+\text{の場合})\\
\, 2\cos\alpha\,\sin\beta &(-\text{の場合})
\end{cases}
\end{aligned}
\begin{aligned}
&\cos(\alpha + \beta) \pm \cos(\alpha - \beta) \\
&=
\begin{cases}
\, 2\cos\alpha\,\cos\beta &(+\text{の場合})\\
\, -2\sin\alpha\,\sin\beta &(-\text{の場合})
\end{cases}
\end{aligned}
において$A=\alpha+\beta$,$B=\alpha-\beta$とすることで導けます:&\cos(\alpha + \beta) \pm \cos(\alpha - \beta) \\
&=
\begin{cases}
\, 2\cos\alpha\,\cos\beta &(+\text{の場合})\\
\, -2\sin\alpha\,\sin\beta &(-\text{の場合})
\end{cases}
\end{aligned}
- $\sin A + \sin B \,\,$$=2\sin\biggl(\dfrac{A+B}{2}\biggr)\cos\biggl(\dfrac{A-B}{2}\biggr)$
- $\sin A - \sin B \,\,$$=2\cos\biggl(\dfrac{A+B}{2}\biggr)\sin\biggl(\dfrac{A-B}{2}\biggr)$
- $\cos A + \cos B \,$$=2\cos\biggl(\dfrac{A+B}{2}\biggr)\cos\biggl(\dfrac{A-B}{2}\biggr)$
- $\cos A - \cos B \,$$=-2\sin\biggl(\dfrac{A+B}{2}\biggr)\sin\biggl(\dfrac{A-B}{2}\biggr)$
三角関数の合成
「三角関数の合成」も簡単に導けます:三角関数の合成
\begin{aligned}
& a\sin\theta+b\cos\theta \\
&=\sqrt{a^2+b^2}\sin(\theta+\alpha)
\end{aligned}
と変形できる.但し,$\alpha$は& a\sin\theta+b\cos\theta \\
&=\sqrt{a^2+b^2}\sin(\theta+\alpha)
\end{aligned}
\begin{aligned}
\cos\alpha
&=\frac{a}{\sqrt{a^2+b^2}} \\
\sin\alpha
&=\frac{b}{\sqrt{a^2+b^2}}
\end{aligned}
で定義される.\cos\alpha
&=\frac{a}{\sqrt{a^2+b^2}} \\
\sin\alpha
&=\frac{b}{\sqrt{a^2+b^2}}
\end{aligned}

\begin{aligned}
& a\sin\theta+b\cos\theta \\
&=\sqrt{a^2+b^2} \\
&\quad \times \biggl( \sin\theta \cdot \frac{a}{\sqrt{a^2+b^2}}
+ \cos\theta \cdot \frac{b}{\sqrt{a^2+b^2}} \biggr) \\
&=\sqrt{a^2+b^2} ( \sin\theta\cos\alpha + \cos\theta \sin\alpha ) \\
&=\sqrt{a^2+b^2}\sin(\theta+\alpha)
\end{aligned}
但し,三辺が$a$,$b$,$\sqrt{a^2+b^2}$の直角三角形を考えて,$\cos\alpha=\dfrac{a}{\sqrt{a^2+b^2}}$,$\sin\alpha=\dfrac{b}{\sqrt{a^2+b^2}}$とした.//& a\sin\theta+b\cos\theta \\
&=\sqrt{a^2+b^2} \\
&\quad \times \biggl( \sin\theta \cdot \frac{a}{\sqrt{a^2+b^2}}
+ \cos\theta \cdot \frac{b}{\sqrt{a^2+b^2}} \biggr) \\
&=\sqrt{a^2+b^2} ( \sin\theta\cos\alpha + \cos\theta \sin\alpha ) \\
&=\sqrt{a^2+b^2}\sin(\theta+\alpha)
\end{aligned}
何に使われるか
冒頭でも触れたように,「三角関数」の応用範囲はとても広いです.- ベクトルで役立つ!
- ベクトルの成分には三角関数が現れます.これは,三角関数の定義に「射影」が用いられていることによります.
- 複素数で役立つ!
- オイラーの公式:$e^{i\theta}=\cos\theta + i\sin\theta$から,複素数と三角関数は密接な関係にあります.
- 積分で役立つ!
- 三角関数に変数変換することで計算できる例が多く存在します.
- 物理で役立つ!
- ベクトルは物理で必須のツールであるため,三角関数の理解は物理の理解にも繋がります.
- 三角関数は「波」を表す関数です.したがって,波動現象の理解には欠かすことができません.