POINT
単純な「連立方程式」の問題ですが，一般解は少し複雑な形になります．
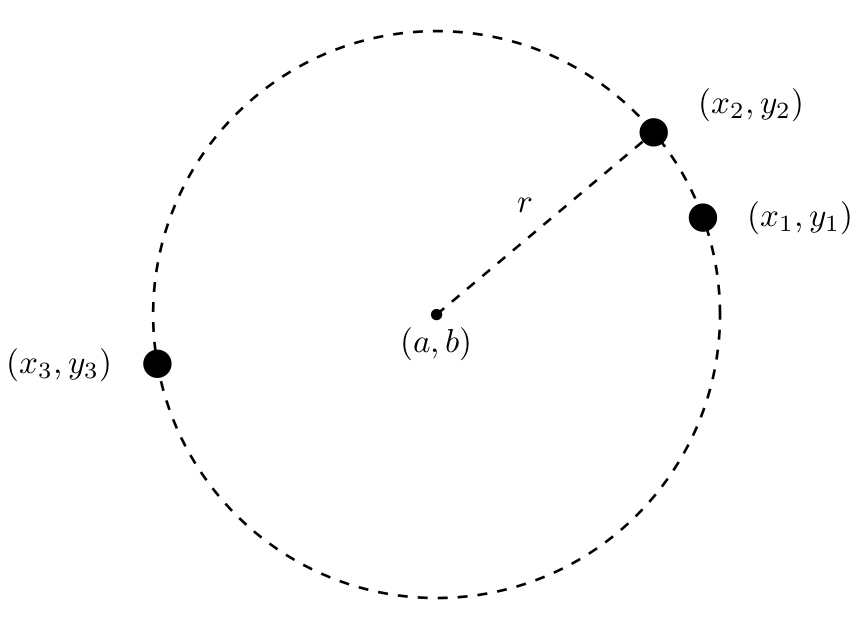
- 円の通る3点から中心・半径を求める一般式を導出する．
- 計算フォーム・Excelにコピペして使えるフォーマットもあります．
計算フォーム
計算結果だけ知りたい場合は，次の計算フォームを利用してください（*1）：| 1点目 | $x_1=$ | $y_1=$ |
|---|---|---|
| 2点目 | $x_2=$ | $y_2=$ |
| 3点目 | $x_3=$ | $y_3=$ |
| 中心$(a,b)=$ | 半径 $r=$ |
Excel用フォーマット
ExcelやGoogle スプレッドシートを使って計算したい方は，以下をコピペしてください（A1のセルに貼り付け）：| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 入力 | 途中計算 | 中心 | 半径 | ||||||||||||
| x1 | y1 | x2 | y2 | x3 | y3 | α | β | γ | δ | |X1|^2 - |X2|^2 | |X2|^2 - |X3|^2 | 2(αδ-βγ) | a | b | r |
| 0 | 0 | 1 | 1 | 2 | 0 | =A3-C3 | =B3-D3 | =C3-E3 | =D3-F3 | =(A3^2 + B3^2) - (C3^2 + D3^2) | =(C3^2 + D3^2) - (E3^2 + F3^2) | =2*(G3*J3-H3*I3) | =(J3*K3 - H3*L3)/M3 | =(-I3*K3 + G3*L3)/M3 | =SQRT((A3-N3)^2 + (B3-O3)^2) |
導出
円の方程式
中心$(a,b)$，半径$r$の円は\begin{aligned}
(x-a)^2+(y-b)^2=r^2
\end{aligned}
という方程式を満たす$(x,y)$で与えられます．(x-a)^2+(y-b)^2=r^2
\end{aligned}
3つの未知数（パラメータ）
- $a$（中心の$x$座標）
- $b$（中心の$y$座標）
- $r$（円の半径）
を決めるためには，3つの方程式が必要です．したがって，円の通る3点$(x_1,y_1)$, $(x_2,y_2)$, $(x_3,y_3)$を与えれば円の方程式を決定することができます．
まずは，結果を与えておきます：
3点を通る円の中心と半径
3点$\{\boldsymbol{X}_i=(x_i,y_i)\}_{i=1,2,3}$を通る円の中心$(a,b)$は
円の半径$r$は
\begin{aligned}
\begin{pmatrix}
a \\
b
\end{pmatrix}
=&\frac{1}{2(\alpha\delta-\beta\gamma)} \times \\
&\quad
\begin{pmatrix}
\delta &-\beta \\
-\gamma&\alpha
\end{pmatrix}
\begin{pmatrix}
|\boldsymbol{X}_1|^2-|\boldsymbol{X}_2|^2\\
|\boldsymbol{X}_2|^2-|\boldsymbol{X}_3|^2
\end{pmatrix}
\end{aligned}
で与えられる．但し，\begin{pmatrix}
a \\
b
\end{pmatrix}
=&\frac{1}{2(\alpha\delta-\beta\gamma)} \times \\
&\quad
\begin{pmatrix}
\delta &-\beta \\
-\gamma&\alpha
\end{pmatrix}
\begin{pmatrix}
|\boldsymbol{X}_1|^2-|\boldsymbol{X}_2|^2\\
|\boldsymbol{X}_2|^2-|\boldsymbol{X}_3|^2
\end{pmatrix}
\end{aligned}
\begin{aligned}
\begin{pmatrix}
\alpha &\beta \\
\gamma&\delta
\end{pmatrix}
&=
\begin{pmatrix}
x_1-x_2 & y_1-y_2 \\
x_2-x_3 & y_2-y_3
\end{pmatrix} \\[1em]
|\boldsymbol{X}_i|^{2} &= x_{i}^{2} + y_{i}^{2}
\end{aligned}
である．\begin{pmatrix}
\alpha &\beta \\
\gamma&\delta
\end{pmatrix}
&=
\begin{pmatrix}
x_1-x_2 & y_1-y_2 \\
x_2-x_3 & y_2-y_3
\end{pmatrix} \\[1em]
|\boldsymbol{X}_i|^{2} &= x_{i}^{2} + y_{i}^{2}
\end{aligned}
円の半径$r$は
\begin{aligned}
r=\sqrt{(x_i-a)^2 + (y_i-b)^2}
\end{aligned}
で計算することができる（$i$は$1,2,3$のうちいずれか一つ）．r=\sqrt{(x_i-a)^2 + (y_i-b)^2}
\end{aligned}
円の中心
円の通る3点$(x_1,y_1)$, $(x_2,y_2)$, $(x_3,y_3)$を与えたことで，未知数$a,b,r$に関する連立方程式\begin{aligned}
\begin{cases}
\,(x_1-a)^2+(y_1-b)^2=r^2 &\qquad\text{(1)} \\
\,(x_2-a)^2+(y_2-b)^2=r^2 &\qquad\text{(2)}\\
\,(x_3-a)^2+(y_3-b)^2=r^2 &\qquad\text{(3)}
\end{cases}
\end{aligned}
が得られます．これは未知数$a,b,r$に関する2次式であるため，このままでは扱いにくい形です．\begin{cases}
\,(x_1-a)^2+(y_1-b)^2=r^2 &\qquad\text{(1)} \\
\,(x_2-a)^2+(y_2-b)^2=r^2 &\qquad\text{(2)}\\
\,(x_3-a)^2+(y_3-b)^2=r^2 &\qquad\text{(3)}
\end{cases}
\end{aligned}
ここで「式( i )$-$式( j )」とすれば
\begin{aligned}
&(x_i+x_j-2a)(x_i-x_j) \\
&\quad +(y_i+y_j-2b)(y_i-y_j) = 0
\end{aligned}
と未知数$a,b,r$に関する2次式を消去することができます（*2）．これを整理すると&(x_i+x_j-2a)(x_i-x_j) \\
&\quad +(y_i+y_j-2b)(y_i-y_j) = 0
\end{aligned}
\begin{aligned}
&(x_i-x_j)a + (y_i-y_j)b \\
&\quad = \frac{1}{2}\left[(x_i^2-x_j^2) + (y_i^2-y_j^2)\right]
\end{aligned}
となります．&(x_i-x_j)a + (y_i-y_j)b \\
&\quad = \frac{1}{2}\left[(x_i^2-x_j^2) + (y_i^2-y_j^2)\right]
\end{aligned}
未知数が$a,b$の2つに減ったため，必要な方程式の数は2つになります．したがって，上の式で$(i,j)=(1,2)$，$(i,j)=(2,3)$として得られる
\begin{aligned}
\begin{cases}
&\!\!\! (x_1-x_2)a + (y_1-y_2)b \\
&\qquad = \frac{1}{2}\left[(x_1^2-x_2^2) + (y_1^2-y_2^2)\right] \\
&\!\!\! (x_2-x_3)a + (y_2-y_3)b \\
&\qquad = \frac{1}{2}\left[(x_2^2-x_3^2) + (y_2^2-y_3^2)\right]
\end{cases}
\end{aligned}
を解けば$a,b$を求めることができます．\begin{cases}
&\!\!\! (x_1-x_2)a + (y_1-y_2)b \\
&\qquad = \frac{1}{2}\left[(x_1^2-x_2^2) + (y_1^2-y_2^2)\right] \\
&\!\!\! (x_2-x_3)a + (y_2-y_3)b \\
&\qquad = \frac{1}{2}\left[(x_2^2-x_3^2) + (y_2^2-y_3^2)\right]
\end{cases}
\end{aligned}
これは，行列の形で書き直すと
\begin{aligned}
&\!\!\!
\begin{pmatrix}
x_1-x_2 & y_1-y_2 \\
x_2-x_3 & y_2-y_3
\end{pmatrix}
\begin{pmatrix}
a \\
b
\end{pmatrix}\\
&\qquad\qquad =\frac{1}{2}
\begin{pmatrix}
|\boldsymbol{X}_1|^2-|\boldsymbol{X}_2|^2\\
|\boldsymbol{X}_2|^2-|\boldsymbol{X}_3|^2
\end{pmatrix}
\end{aligned}
となります（$\boldsymbol{X}_i=(x_i,y_i)$としました．$|\boldsymbol{X}_i|$はベクトルの大きさです（つまり$|\boldsymbol{X}_i|^2=x_i^2+y_i^2$））．&\!\!\!
\begin{pmatrix}
x_1-x_2 & y_1-y_2 \\
x_2-x_3 & y_2-y_3
\end{pmatrix}
\begin{pmatrix}
a \\
b
\end{pmatrix}\\
&\qquad\qquad =\frac{1}{2}
\begin{pmatrix}
|\boldsymbol{X}_1|^2-|\boldsymbol{X}_2|^2\\
|\boldsymbol{X}_2|^2-|\boldsymbol{X}_3|^2
\end{pmatrix}
\end{aligned}
このままでは見づらいので，左辺の$2\times2$行列を
\begin{aligned}
M=
\begin{pmatrix}
\alpha &\beta \\
\gamma&\delta
\end{pmatrix}
\end{aligned}
としましょう．よく知られているように，$M$の逆行列はM=
\begin{pmatrix}
\alpha &\beta \\
\gamma&\delta
\end{pmatrix}
\end{aligned}
\begin{aligned}
M^{-1}=\frac{1}{\alpha\delta-\beta\gamma}
\begin{pmatrix}
\delta &-\beta \\
-\gamma&\alpha
\end{pmatrix}
\end{aligned}
なので，未知数$a,b$はM^{-1}=\frac{1}{\alpha\delta-\beta\gamma}
\begin{pmatrix}
\delta &-\beta \\
-\gamma&\alpha
\end{pmatrix}
\end{aligned}
\begin{aligned}
\begin{pmatrix}
a \\
b
\end{pmatrix}
=&\frac{1}{2(\alpha\delta-\beta\gamma)} \times \\
&\quad
\begin{pmatrix}
\delta &-\beta \\
-\gamma&\alpha
\end{pmatrix}
\begin{pmatrix}
|\boldsymbol{X}_1|^2-|\boldsymbol{X}_2|^2\\
|\boldsymbol{X}_2|^2-|\boldsymbol{X}_3|^2
\end{pmatrix}
\end{aligned}
であることがわかりました．\begin{pmatrix}
a \\
b
\end{pmatrix}
=&\frac{1}{2(\alpha\delta-\beta\gamma)} \times \\
&\quad
\begin{pmatrix}
\delta &-\beta \\
-\gamma&\alpha
\end{pmatrix}
\begin{pmatrix}
|\boldsymbol{X}_1|^2-|\boldsymbol{X}_2|^2\\
|\boldsymbol{X}_2|^2-|\boldsymbol{X}_3|^2
\end{pmatrix}
\end{aligned}
円の半径
上で円の中心$(a,b)$がわかったので，円の方程式から\begin{aligned}
r=\sqrt{(x_i-a)^2 + (y_i-b)^2}
\end{aligned}
と計算することができます（$(x_i,y_i)$は，3点$(x_1,y_1)$, $(x_2,y_2)$, $(x_3,y_3)$の中の任意の1点）．r=\sqrt{(x_i-a)^2 + (y_i-b)^2}
\end{aligned}
別解：垂直二等分線の交点を計算
円の中心は，2直線- $l_{12}$：2点$(x_1,y_1)$と$(x_2,y_2)$の垂直二等分線
- $l_{23}$：2点$(x_2,y_2)$と$(x_3,y_3)$の垂直二等分線
の交点として求めることができます．
【Step.1：直線$l_{ij}$の方程式を求める】
直線$l_{ij}$の方程式を
\begin{aligned}
y=ax+b
\end{aligned}
として，未知数$a,b$を決定しましょう．y=ax+b
\end{aligned}
【Step.1-(1)：直線$l_{ij}$の傾き$a$を求める】
直線$l_{ij}$は「2点$(x_i,y_i)$と$(x_j,y_j)$を通る直線」と直交します．「2点$(x_i,y_i)$と$(x_j,y_j)$を通る直線」の傾きは
\begin{aligned}
\textcolor{red}{\frac{y_i-y_j}{x_i-x_j}}
\end{aligned}
ですから，直線$l_{ij}$の傾き$a$は\textcolor{red}{\frac{y_i-y_j}{x_i-x_j}}
\end{aligned}
\begin{aligned}
a\cdot \textcolor{red}{\frac{y_i-y_j}{x_i-x_j}} =-1
\end{aligned}
を満たします．したがって，a\cdot \textcolor{red}{\frac{y_i-y_j}{x_i-x_j}} =-1
\end{aligned}
\begin{aligned}
a=-\frac{x_i-x_j}{y_i-y_j}
\end{aligned}
であることがわかります．a=-\frac{x_i-x_j}{y_i-y_j}
\end{aligned}
【Step.1-(2)：直線$l_{ij}$の切片$b$を求める】
また，直線$l_{ij}$は2点$(x_i,y_i)$と$(x_j,y_j)$の中点
\begin{aligned}
\left(\frac{x_i+x_j}{2},\frac{y_i+y_j}{2}\right)
\end{aligned}
を通るので$y=ax+b$に代入すると\left(\frac{x_i+x_j}{2},\frac{y_i+y_j}{2}\right)
\end{aligned}
\begin{aligned}
\frac{y_i+y_j}{2} = -\frac{x_i-x_j}{y_i-y_j}\cdot \frac{x_i+x_j}{2} + b
\end{aligned}
が成り立ちます．これを$b$について解けば\frac{y_i+y_j}{2} = -\frac{x_i-x_j}{y_i-y_j}\cdot \frac{x_i+x_j}{2} + b
\end{aligned}
\begin{aligned}
b&=\frac{y_i+y_j}{2} + \frac{x_i-x_j}{y_i-y_j}\cdot \frac{x_i+x_j}{2} \\
&=\frac{(x_i^2+y_i^2)-(x_j^2+y_j^2)}{2(y_i-y_j)}
\end{aligned}
となります．b&=\frac{y_i+y_j}{2} + \frac{x_i-x_j}{y_i-y_j}\cdot \frac{x_i+x_j}{2} \\
&=\frac{(x_i^2+y_i^2)-(x_j^2+y_j^2)}{2(y_i-y_j)}
\end{aligned}
以上より，直線$l_{ij}$の方程式が
\begin{aligned}
y=-\frac{x_i-x_j}{y_i-y_j} x
+\frac{(x_i^2+y_i^2)-(x_j^2+y_j^2)}{2(y_i-y_j)}
\end{aligned}
であることがわかりました（注：これは1つ目の方法で円の方程式から求めた式とおなじものです）．y=-\frac{x_i-x_j}{y_i-y_j} x
+\frac{(x_i^2+y_i^2)-(x_j^2+y_j^2)}{2(y_i-y_j)}
\end{aligned}
【Step.2：円の中心座標$(a,b)$を求める】
上で求めた直線$l_{ij}$の方程式に$(i,j)=(1,2),(2,3)$を代入して2直線$l_{12}$, $l_{23}$の方程式を作ります．2式を連立して$x,y$について解けば，円の中心座標$(a,b)$を求めることができます．
【Step.3：円の半径$r$を求める】
上で円の中心$(a,b)$がわかったので，円の方程式から
\begin{aligned}
r=\sqrt{(x_i-a)^2 + (y_i-b)^2}
\end{aligned}
と計算することができます（$(x_i,y_i)$は，3点$(x_1,y_1)$, $(x_2,y_2)$, $(x_3,y_3)$の中の任意の1点）．
r=\sqrt{(x_i-a)^2 + (y_i-b)^2}
\end{aligned}
