ベイズの定理は,条件付き確率の計算において頻繁に使われます.しかし,実は状況を表に整理することで,ベイズの定理の公式を覚えなくても簡単に同じ結果が得られます.この記事では,表を使った「ベイズの定理」の簡単な理解と計算方法を解説します.
POINT
条件付き確率の状況を表に整理すると,ベイズの定理を明示的に使うことなく同じ結果が得られます.- 条件付き確率の問題を表にまとめると,ベイズの定理を覚えなくても条件付き確率を計算できる.
ベイズの定理の仕組みをベン図で直感的に理解したい場合は,以下の記事を合わせて読むことでさらに理解が深まります.
➡ベン図でわかる条件付き確率とベイズの定理 - Notes_JP
ベイズの定理を使った例題:Wikipediaの「薬物検査」
Wikipediaの例で解説します.Wikipediaでは,ベイズの定理を使った方法が記載されているので,以下の方法と比べてみてください.ベイズの定理 - Wikipedia
まとめると,つぎの内容です.
Wikipedia「薬物検査」
この薬物検査では,薬物の使用者の99%が陽性になり,非使用者の99%が陰性になる.また,社会全体の薬物使用者は0.5%であることがわかっている.この薬物検査で陽性だった人が薬物使用者である確率を求めよ.
解法
この問題は,次のように図示できます.
この表に,各事象の起きる確率を記入すると,以下になります.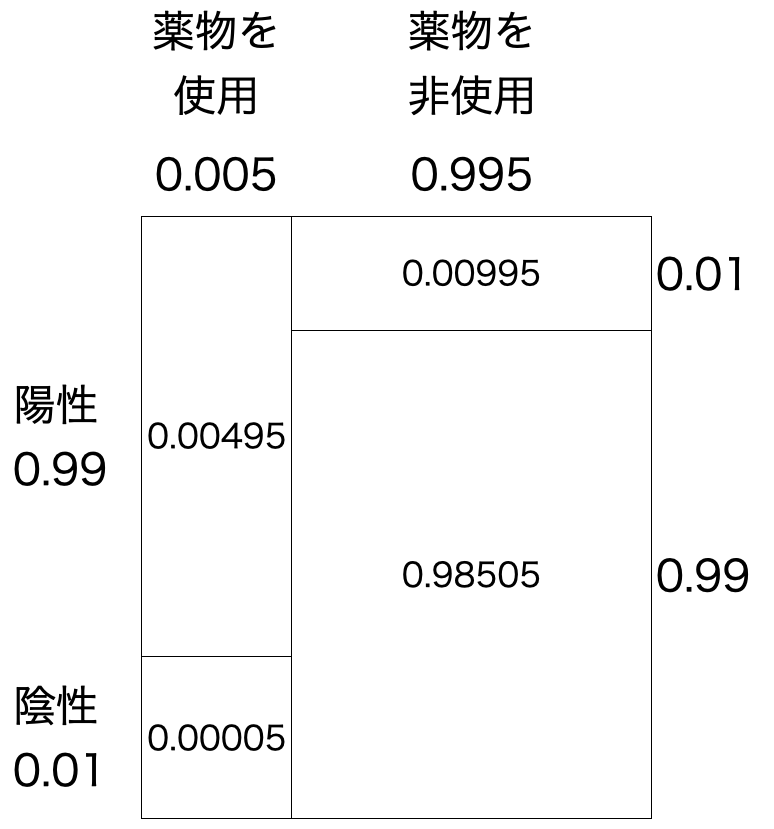
以上より,次のようにして確率を計算できます.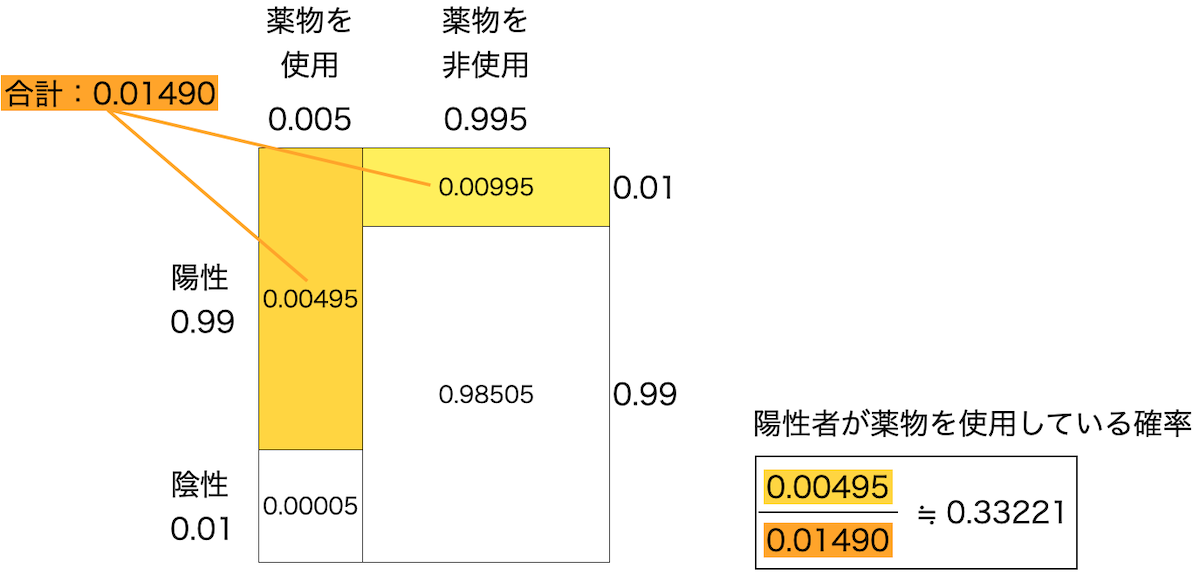
何一つ公式を覚えず,簡単に計算できますね.
ベイズの定理との対応
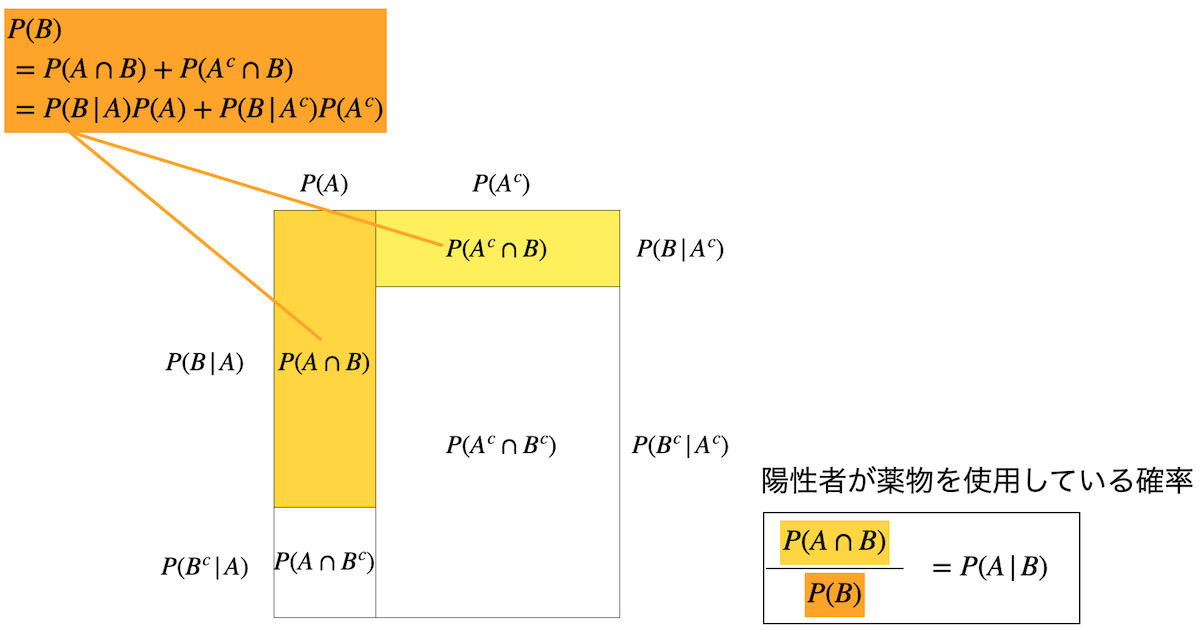
上の表を,条件付き確率の言葉で置き換えたのが以下です.ベイズの定理の一般的な数式は,
\begin{aligned}
P(A|B) = \frac{P(B|A)P(A)}{P(B)}
\end{aligned}
となりますが,これは表と完全に対応しています.表を用いることで,この数式を意識せずに計算できるのです.P(A|B) = \frac{P(B|A)P(A)}{P(B)}
\end{aligned}
実際は,こうして記号で置き換えずに,上でやったように数値を直接書き込んで行くほうが簡単です.