TikZ実例集〜2Dグラフ編

TikZで作った図（2D）

POINT

• TikZで作成した図（2D）のソースコードを紹介！
• 3次元編はこちら

ブログ記事のためにTikZで作成した図のTeXコードを，備忘録として残しておきます．

ベクトルの回転（2次元）

ベクトルの回転を説明する図をTeX（TikZ）で作成しました．

作成した図：

この図は，以下の記事で使っています：

▶クリックしてソースコードを表示

\begin{figure}[htbp]
  % 左の図
  \begin{minipage}{0.3\hsize}
    \begin{center}
      \begin{tikzpicture}[scale=2]
        % 座標軸
        \draw [thick, -stealth](-0.5,0)--(3/2,0) node [anchor=north]{$x$};
        \draw [thick, -stealth](0,-0.5)--(0,3/2) node [anchor=east]{$y$};
        \node [anchor=north east] at (0,0) {O};        
        % 補助線
        \draw [dashed](0,{sqrt(3)/2})--(1/2,{sqrt(3)/2});
        \draw [dashed](1/2,0)--(1/2,{sqrt(3)/2});
        \draw [thin,->](0:1/4) arc (0:60:1/4);
        \node at(40:1/4) [anchor=west]{$\theta$}; %極座標表示：(θ:r)      
        % ベクトル
        \draw [very thick, -stealth, blue](0,0)--(1,0)node [anchor=north]{(1,0)};
        \draw [very thick, -stealth, blue](0,0)--(1/2,{sqrt(3)/2})node [anchor=west]{($\cos\theta,\sin\theta$)};   
      \end{tikzpicture}
    \end{center}
  \end{minipage}
  % 右の図
  \begin{minipage}{0.3\hsize}
    \begin{center}
      \begin{tikzpicture}[scale=2]
        % 座標軸
        \draw [thick, -stealth](-3/2,0)--(1/2,0) node [anchor=north]{$x$};
        \draw [thick, -stealth](0,-0.5)--(0,3/2) node [anchor=east]{$y$};
        \node [anchor=north east] at (0,0) {O};      
        % 補助線
        \draw [dashed](0,1/2)--(-{sqrt(3)/2},1/2);
        \draw [dashed](-{sqrt(3)/2},0)--(-{sqrt(3)/2},1/2);
        \draw [thin,->](90:1/4) arc (90:150:1/4);
        \node at(130:1/4) [anchor=south]{$\theta$}; %極座標表示：(θ:r)   
        % ベクトル
        \draw [very thick, -stealth, red](0,0)--(0,1)node [anchor=west]{(0,1)};
        \draw [very thick, -stealth, red](0,0)--(-{sqrt(3)/2},1/2)node [anchor=east]{($-\sin\theta,\cos\theta$)};     
      \end{tikzpicture}
    \end{center}
  \end{minipage}
\end{figure}

参考記事：

• 「基本的な使い方」，「オプション」
  • Home - TikZを使ってみよう！ - Cute.Guides at 九州大学 Kyushu University
• nodeの追加方法
  • TeXのTikZによるグラフ描画 - 理系ジン
• 図を並べる方法
  • 図の挿入 - [物理のかぎしっぽ]

二項分布

作成した図：

二項分布

この図は，以下の記事で使っています：

▶クリックしてソースコードを表示

\pgfplotsset{
  standard/.style={%Axis format configuration
    axis x line=middle,
    axis y line=middle,
    enlarge x limits=0.15,
    enlarge y limits=0.15,
    every axis x label/.style={at={(current axis.right of origin)},anchor=north west},
    every axis y label/.style={at={(current axis.above origin)},anchor=north east},
  }
}

\begin{figure}%Sampled sine squence
  \begin{tikzpicture}[scale=1]
    \begin{axis}[%
        standard,
        domain = 0:50,
        samples = 51,
        xlabel={$k$},
        ylabel={$P(k)$}]
      \addplot+[ycomb,black,thick,mark options={fill=white}] {(factorial(50)/(factorial(50-x)*factorial(x))) * (1/2)^50};
      \addplot[red,only marks,mark options={fill=red,scale=1.2},mark=*] coordinates {
        (0,0)
      };
      \node[pin={[pin distance=1cm]60:{$\dfrac{1}{2^{50}}$}}] at (axis cs:0,0) {};
    \end{axis}
  \end{tikzpicture}
\end{figure}

参考記事：

• pgfplots - What is the best way to produce TikZ picture for discrete signals? - TeX - LaTeX Stack Exchange
• tikz pgf - Combination Function with Factorial - Not correct result - Pgfplots - TeX - LaTeX Stack Exchange（階乗の計算）
• PGFPlots Gallery

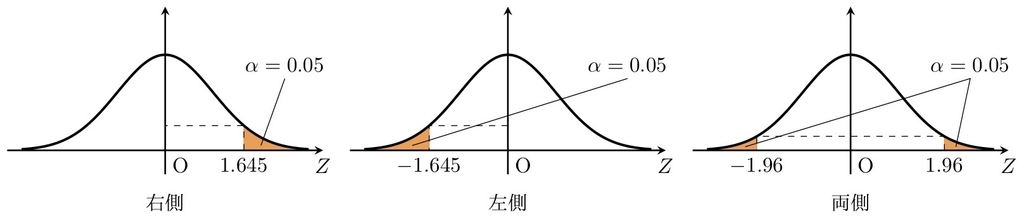
棄却域（統計的仮説検定）

作成した図：

棄却域の種類

この図は，以下の記事で使っています：

▶クリックしてソースコードを表示

\begin{figure}[htbp]
  \begin{center}
    \begin{tabular}{c}
      % 左の図
      \begin{minipage}{0.33\hsize}
        \begin{center}
          \begin{tikzpicture} [xscale = 0.8, yscale = 4]
            % 塗りつぶし
            \filldraw [orange, opacity=.75, domain=1.645:3, samples=200](1.645,0)--plot(\x, {exp((-(\x)^2)/2)/(sqrt(2*pi))})--(3,0);
            
            % 座標軸
            \draw [thick, -stealth](-3.3,0)--(3.3,0) node [anchor=north]{$Z$};
            \draw [thick, -stealth](0,-0.1)--(0,0.6) node [anchor=east]{$$};
            \node [anchor=north west] at (0,0) {O};
            \node [anchor=north] at (0,-0.15) {右側};
            
            % 正規分布
            \draw [very thick, domain=-3:3, samples=200] plot(\x, {exp((-(\x)^2)/2)/(sqrt(2*pi))});
            
            % 補助線
            \draw [dashed](1.645,0) node [anchor=north]{$1.645$}--(1.645,{exp((-(1.645)^2)/2)/(sqrt(2*pi))})--(0,{exp((-(1.645)^2)/2)/(sqrt(2*pi))});
            
            % 説明
            \draw [thin](2, 0.02)--(2.5,0.3) node [anchor=south]{$\alpha=0.05$};
          \end{tikzpicture}
        \end{center}
      \end{minipage}
      % 中央の図
      \begin{minipage}{0.33\hsize}
        \begin{center}
          \begin{tikzpicture} [xscale = 0.8, yscale = 4]
            %塗りつぶし
            \filldraw [orange, opacity=.75, domain=-1.645:-3, samples=200](-1.645,0)--plot(\x, {exp((-(\x)^2)/2)/(sqrt(2*pi))})--(-3,0);
            
            % 座標軸
            \draw [thick, -stealth](-3.3,0)--(3.3,0) node [anchor=north]{$Z$};
            \draw [thick, -stealth](0,-0.1)--(0,0.6) node [anchor=east]{$$};
            \node [anchor=north west] at (0,0) {O};
            \node [anchor=north] at (0,-0.15) {左側};
            
            % 正規分布
            \draw [very thick, domain=-3:3, samples=200] plot(\x, {exp((-(\x)^2)/2)/(sqrt(2*pi))});
            
            % 補助線
            \draw [dashed] (0,{exp((-(-1.645)^2)/2)/(sqrt(2*pi))})--(-1.645,{exp((-(-1.645)^2)/2)/(sqrt(2*pi))})--(-1.645,0) node[anchor=north]{$-1.645$};            
            
            % 説明
            \draw [thin](-2, 0.02)--(2.5,0.3) node [anchor=south]{$\alpha=0.05$};                                 
          \end{tikzpicture}
        \end{center}
      \end{minipage}
      % 右の図
      \begin{minipage}{0.33\hsize}
        \begin{center}
          \begin{tikzpicture} [xscale = 0.8, yscale = 4]
            %塗りつぶし
            \filldraw [orange, opacity=.75, domain=1.96:3, samples=200](1.96,0)--plot(\x, {exp((-(\x)^2)/2)/(sqrt(2*pi))})--(3,0);
            \filldraw [orange, opacity=.75, domain=-1.96:-3, samples=200](-1.96,0)--plot(\x, {exp((-(\x)^2)/2)/(sqrt(2*pi))})--(-3,0);
            
            % 座標軸
            \draw [thick, -stealth](-3.3,0)--(3.3,0) node [anchor=north]{$Z$};
            \draw [thick, -stealth](0,-0.1)--(0,0.6) node [anchor=east]{$$};
            \node [anchor=north west] at (0,0) {O};
            \node [anchor=north] at (0,-0.15) {両側};
            
            % 正規分布
            \draw [very thick, domain=-3:3, samples=200] plot(\x, {exp((-(\x)^2)/2)/(sqrt(2*pi))});
            
            % 補助線
            \draw [dashed](1.96,0) node [anchor=north]{$1.96$}--(1.96,{exp((-(1.96)^2)/2)/(sqrt(2*pi))})--(-1.96,{exp((-(-1.96)^2)/2)/(sqrt(2*pi))})--(-1.96,0) node[anchor=north]{$-1.96$};            
            
            % 説明
            \draw [thin](-2.2, 0.015)--(2.5,0.3) node [anchor=south]{$\alpha=0.05$}--(2.2, 0.015);                      
          \end{tikzpicture}      
        \end{center}
      \end{minipage}
    \end{tabular}
  \end{center}
\end{figure}

ベン図

作成した図：

条件付き確率

---

事象AとBどちらが起こるかによって確率は異なる．

---

偶数がでたと知った上で，2が出る確率．

この図は，以下の記事で使っています：

参考記事の内容を殆どそのまま流用しているため，ソースコードは省略します．

参考記事：

• tikz pgf - Label intersection of 3 sets - TeX - LaTeX Stack Exchange

ポートフォリオ理論

作成した図：

2資産のポートフォリオ

---

3資産のポートフォリオ

---

無差別曲線

この図は，以下の記事で使っています：

流用性はあまり高くないと思うので，ソースコードは省略します．
ここでは「グラフも簡単にかける！」ということを紹介するに留めておきます．

ユークリッドの互除法

次の記事の図はTikZで作成したものです．

ユークリッドの互除法