コイントスを繰り返して,あるパターンが初めて現れるまでには,平均して何回かかるだろうか?
一見,表 (H - Head) と裏 (T - Tail) がそれぞれ確率$\dfrac{1}{2}$で出るコインなら,すべてのパターンの期待値は同じだと思うかもしれないが,実は大きく異なる.例えば,「HHH」や「TTT」が平均14回もかかるのに対し,「HHT」や「HTT」は平均8回で済む:
| 平均回数(期待値) | パターン |
|---|---|
| 14回 | HHH, TTT |
| 10回 | HTH, THT |
| 8回 | HHT, HTT, THH, TTH |
なぜ,このような違いが生じるのか?
本記事では,この理由をマルコフ連鎖の考え方を使って詳しく解説する.
また,条件付き期待値による計算結果(➡[A] こちらの記事を参照)と一致することを確認する.
問題設定
コインの表 (H - Head) が出る確率を$p$,裏 (T - Tail) が出る確率を$1-p$として,「長さ3のコインのパターンが初めて現れるまでの回数の期待値」を計算する.マルコフ連鎖による定式化
この問題をマルコフ連鎖を使って考える方法を示す.状態遷移図と推移確率
状態間の遷移を図に表したものを状態遷移図と呼び,状態間の遷移の確率を行列で表したものを推移確率行列$P$という.推移確率行列$P$の$(i, j)$成分$p_{ij}$は,状態$i$から状態$j$への推移確率を表す.例えば,「HHH」が出るまでの状態遷移図と推移確率行列$P$は以下で表される:
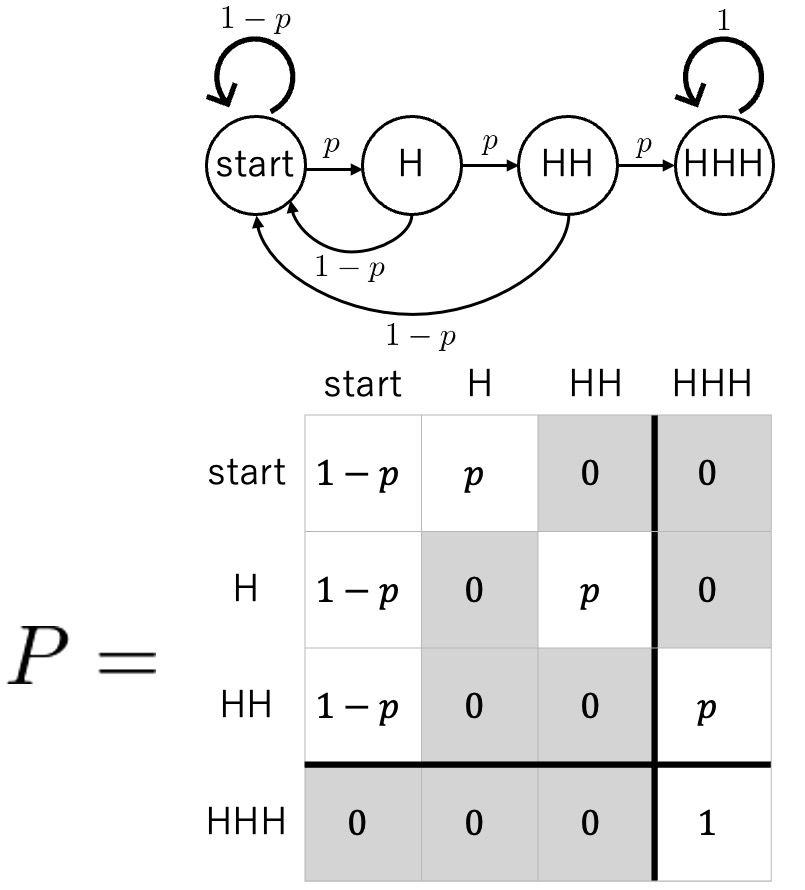
推移確率行列の一般形
一度入ったら抜け出せない状態を吸収状態とよぶ.上の例では,「HHH」が初めて出たらその状態に留まり続けるため,「HHH」が吸収状態である.同様に,HHH以外のパターンでも,パターンが出たあとはその状態に留まる.
この問題の推移確率行列は以下の形を取る.
P&=\left(\begin{array} {ccc:c}
& & & \\
&U&&R \\
&&& \\ \hdashline
&0&&I
\end{array}\right)\\
\end{aligned}
| 行列 | 意味 |
|---|---|
| $U$ | パターンが出ていない状態内での遷移 |
| $R$ | パターンが出ていない状態からパターンが出た状態への遷移 |
| $I$ (単位行列) | 吸収状態 (パターンが出たあとはその状態に留まる) |
期待値の一般公式
パターンが出ていない状態$i$から始めて,$m$回目に始めてパターンが出る遷移はU^{m-1} R \quad(m=1, 2, 3, \ldots)
\end{aligned}
よって,初めてパターンが出るまでの回数の期待値は
\sum_{m=1}^{\infty} m U^{m-1} R
= \bigl[(I - U)^{-1}\bigr]^{2} R
\end{aligned}
特に,$R$の列数が1の場合は,次の簡単な式で計算可能である:
(I - U)^{-1}
\begin{pmatrix}
1 \\
1 \\
\vdots \\
1
\end{pmatrix}
\end{aligned}
具体例(各パターンの計算結果)
HHH
推移確率行列はP
&=\left(\begin{array} {ccc:c}
1-p& p & 0 &0 \\
1-p&0&p&0 \\
1-p&0&0&p \\ \hdashline
0&0&0&1
\end{array}\right)
\end{aligned}
したがって,期待値は
\bigl[(I - U)^{-1}\bigr]^{2} R
&= \frac{1}{p^{3}}
\begin{pmatrix}
p^{2} + p + 1 \\
p + 1 \\
1
\end{pmatrix}
\end{aligned}
※WolframAlphaを使って期待値を計算する方法をいくつか挙げておく.
- $(I - U)^{-1} (I - U)^{-1} R$
- $((I - U)^{-1})^{2} R$
- $(I - U)^{-1} \begin{pmatrix} 1 \\ 1 \\ \vdots \\ 1 \end{pmatrix}$
初期状態 (start) から始めた場合の期待値は第1成分
\frac{p^{2} + p + 1}{p^{3}}
\end{aligned}

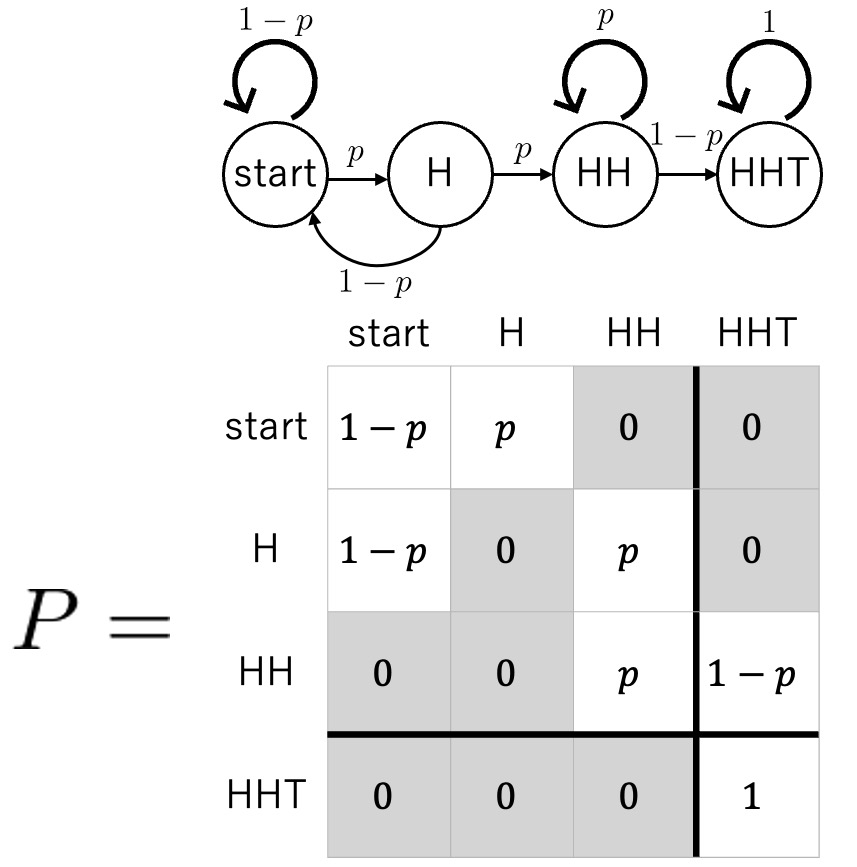
HHT
推移確率行列はP
&=\left(\begin{array} {ccc:c}
1-p& p & 0 &0 \\
1-p&0&p&0 \\
0&0&p&1-p \\ \hdashline
0&0&0&1
\end{array}\right)
\end{aligned}
したがって,WolframAlphaを使って期待値$(I - U)^{-1} \begin{pmatrix} 1 \\ 1 \\ \vdots \\ 1 \end{pmatrix}$を計算すると
\bigl[(I - U)^{-1}\bigr]^{2} R
&= \frac{1}{1-p}
\begin{pmatrix}
\frac{1}{p^{2}} \\
\frac{p^{2}-p+1}{p^{2}} \\
1
\end{pmatrix}
\end{aligned}
初期状態 (start) から始めた場合の期待値は第1成分
\frac{1}{p^{2}(1-p)}
\end{aligned}
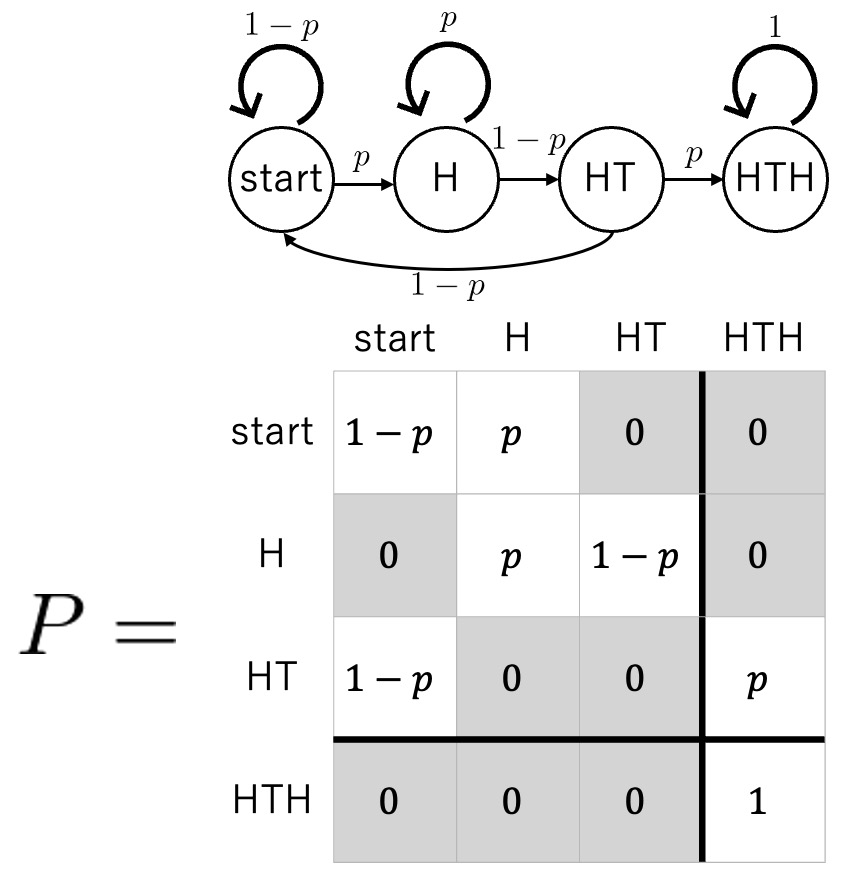
HTH
推移確率行列はP
&=\left(\begin{array} {ccc:c}
1-p& p & 0 &0 \\
0&p&1-p&0 \\
1-p&0&0&p \\ \hdashline
0&0&0&1
\end{array}\right)
\end{aligned}
したがって,WolframAlphaを使って期待値$((I - U)^{-1})^{2} R$を計算すると
\bigl[(I - U)^{-1}\bigr]^{2} R
&= \frac{1}{p^{2}}
\begin{pmatrix}
\frac{-p^{2} + p + 1}{1-p} \\
\frac{1}{1-p} \\
p + 1
\end{pmatrix}
\end{aligned}
初期状態 (start) から始めた場合の期待値は第1成分
\frac{-p^{2} + p + 1}{p^{2}(1-p)}
\end{aligned}
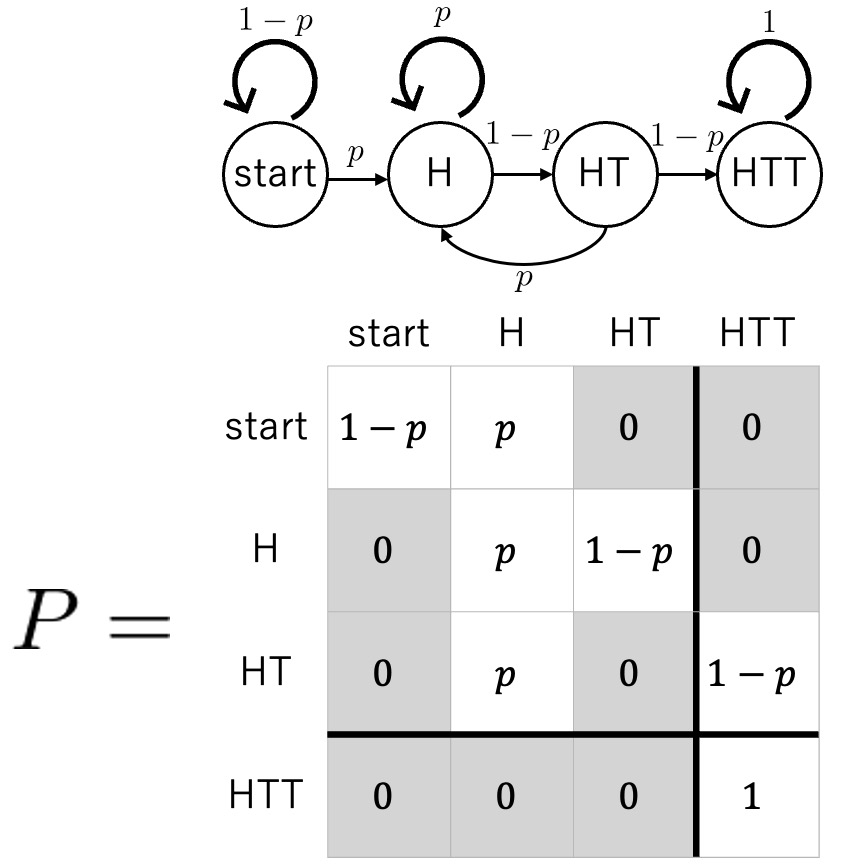
HTT
推移確率行列はP
&=\left(\begin{array} {ccc:c}
1-p& p & 0 &0 \\
0&p&1-p&0 \\
0&p&0&1-p \\ \hdashline
0&0&0&1
\end{array}\right)
\end{aligned}
したがって,WolframAlphaを使って期待値$(I - U)^{-1} \begin{pmatrix} 1 \\ 1 \\ \vdots \\ 1 \end{pmatrix}$を計算すると
\bigl[(I - U)^{-1}\bigr]^{2} R
&= \frac{1}{(1-p)^{2}}
\begin{pmatrix}
\frac{1}{p} \\
2-p \\
1
\end{pmatrix}
\end{aligned}
初期状態 (start) から始めた場合の期待値は第1成分
\frac{1}{p(1-p)^{2}}
\end{aligned}
※記事[A]ではTHHを計算しているので,$p\to 1-p$とする.
まとめ
本記事では,マルコフ連鎖を使ってコイントスで特定パターンが初めて現れるまでの期待値の計算方法を解説した.条件付き期待値を用いた結果とも一致することを確認し,「なぜパターンによって期待値が異なるのか」についても理論的に説明した.2つのパターンのうちどちらが先に出るかという問題も,直感に反する非常に面白い問題である.以下の記事で扱っているので,気になる方はぜひ.
参考文献
付録(詳しい導出方法)
期待値の導出
まず,\lim_{n\to\infty} U^{n}
= 0
\end{aligned}
(I -U) (I + U + U^{2} + \cdots + U^{m-1})
= I - U^{m}
\end{aligned}
\sum_{m=0}^{\infty} U^{m}
= (I - U)^{-1}
\end{aligned}
ここで,(行列値でない)通常の幾何級数と同じように
\sum_{m=1}^{\infty} m U^{m-1}
&= \frac{\partial}{\partial U} \sum_{m=0}^{\infty} U^{m} \\
&= \frac{\partial}{\partial U} (I - U)^{-1} \\
&= (I - U)^{-2}
\end{aligned}
\sum_{m=1}^{\infty} m U^{m-1} R
&= \bigl[(I - U)^{-1}\bigr]^{2} R
\end{aligned}
推移確率行列のn乗とその極限
この記事では使わなかったが,推移確率行列$P$についてP^{n}
&=\left(\begin{array} {ccc:c}
& & & \\
&U^{n}&&\displaystyle \sum_{m=0}^{n} U^{m} R \\
&&& \\ \hdashline
&0&&I
\end{array}\right)\\
& \rightarrow
\left(\begin{array} {ccc:c}
& & & \\
& 0 && (I - U)^{-1} R \\
&&& \\ \hdashline
&0&&I
\end{array}\right) \quad (n\to\infty)
\end{aligned}
