表(H:Head)と裏(T:Tail)がそれぞれ確率$\frac{1}{2}$で出るコインを繰り返し投げるとき,特定のパターン(例:HHHやTTT)が初めて出現するまでの回数の期待値を考えます.
各パターンはどれも同じ確率($1/8$)で出るのに,なぜか現れるまでの平均回数には大きな違いがあります.例えば,「HHH」「TTT」は平均14回,「HTH」「THT」は10回,「HHT」「HTT」などは8回と異なります.
本記事では,各パターンの期待値を分かりやすく計算し,「なぜパターンによって差が生じるのか」についても直感的に解説します.
本記事の方法は,以下の書籍「2. サイコロ遊びにご用心」で紹介されていたものです.
各パターンの期待値一覧
| 平均回数(期待値) | パターン |
|---|---|
| 14回 | HHH, TTT |
| 10回 | HTH, THT |
| 8回 | HHT, HTT, THH, TTH |
準備
いくつかの性質と,記法について準備する.性質
性質1:どのパターンも確率$1/8$で現れる何度もコイントスしてできたH, Tのパターンの列を$a_{1}a_{2}a_{3}\cdots $で表す.このとき,どの連続する3つの出目$a_{i}a_{i+1}a_{i+2}$に着目しても,特定のパターンが出る確率は$1/2^{3} = 1/8$である.
性質2:特定パターンの再出現の期待値は常に8回
さて,上で定めた列$a_{1}a_{2}a_{3}\cdots $を,3つごとにまとめてできた列$b_{1} b_{2} b_{3} \cdots$を$b_{1} = a_{1}a_{2}a_{3}, b_{2} = a_{2}a_{3}a_{4},\ldots$を考える.すると,性質1より,$2^{3} = 8$個のパターンは列$b_{1} b_{2} b_{3} \cdots$に一様に分布する.つまり,あるパターンが$b_{i}$で現れたとすると,次に同じパターンが現れるまでの回数の期待値は$2^{3} = 8$である.列$a_{1}a_{2}a_{3}\cdots $で考えれば,あるパターンが完成してから次に同じパターンが現れるまでのコイントスの回数が$2^{3} = 8$回ということを意味する.
記法
- パターン$X$の長さを$|X|$と表す.例えば,$|HHT| = 3$.
- コインを$|X|$回投げて,パターン$X$がでる確率を$P(X)$と表す.
- 初めてパターン$Y$が出たあと,1回以上コインをトスして,初めてパターン$X$が現れるまでの回数の期待値を$E[X|Y]$と表す(注:$Y$の一部または全部を使ってパターン$X$が完成すれば良い).
パターン別の具体的な期待値の計算方法
HHH(14回)
TTTも同じ.結論から言うと,$2^{3} + 2^{2} + 2^{1} = 14$回と計算できる.
これは,以下のように3つの期待値を順に計算することで得られる.
期待値1)
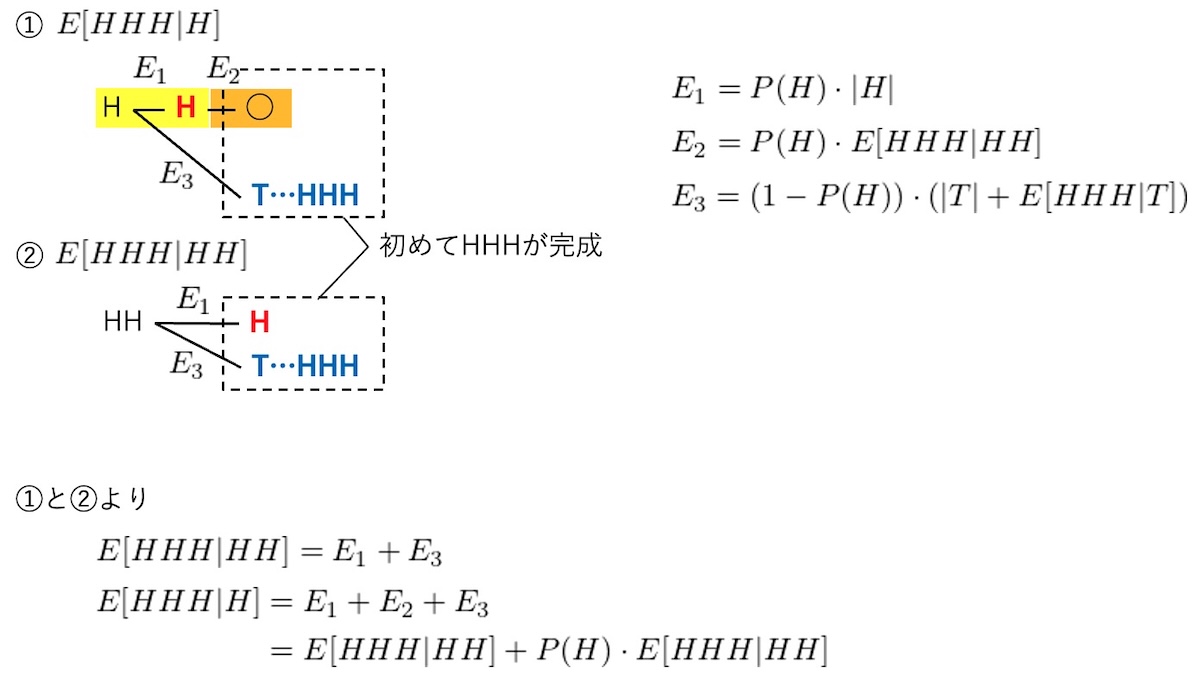
「初めてHHが現れてから」次にHHHが現れるまでの回数の期待値は,HHHが現れてから次にHHHが現れるまでの回数の期待値に等しく,「性質2」から$E[HHH|HH] = E[HHH|HHH] = 2^{3}=8$回.
期待値2)
「初めてHが現れてから」次にHHHが現れるまでの回数の期待値と,期待値1)の差を考える.
- 初めてHHが出た状態では,Hが出るとHHHが完成する
- 「初めてHが現れてから」Hが出ると,初めてHHが出た状態に移行する(パターンが完成しない)
E[HHH | H]
&= E[HHH | HH] + P(H) \cdot E[HHH|HH]
\end{aligned}
期待値3)
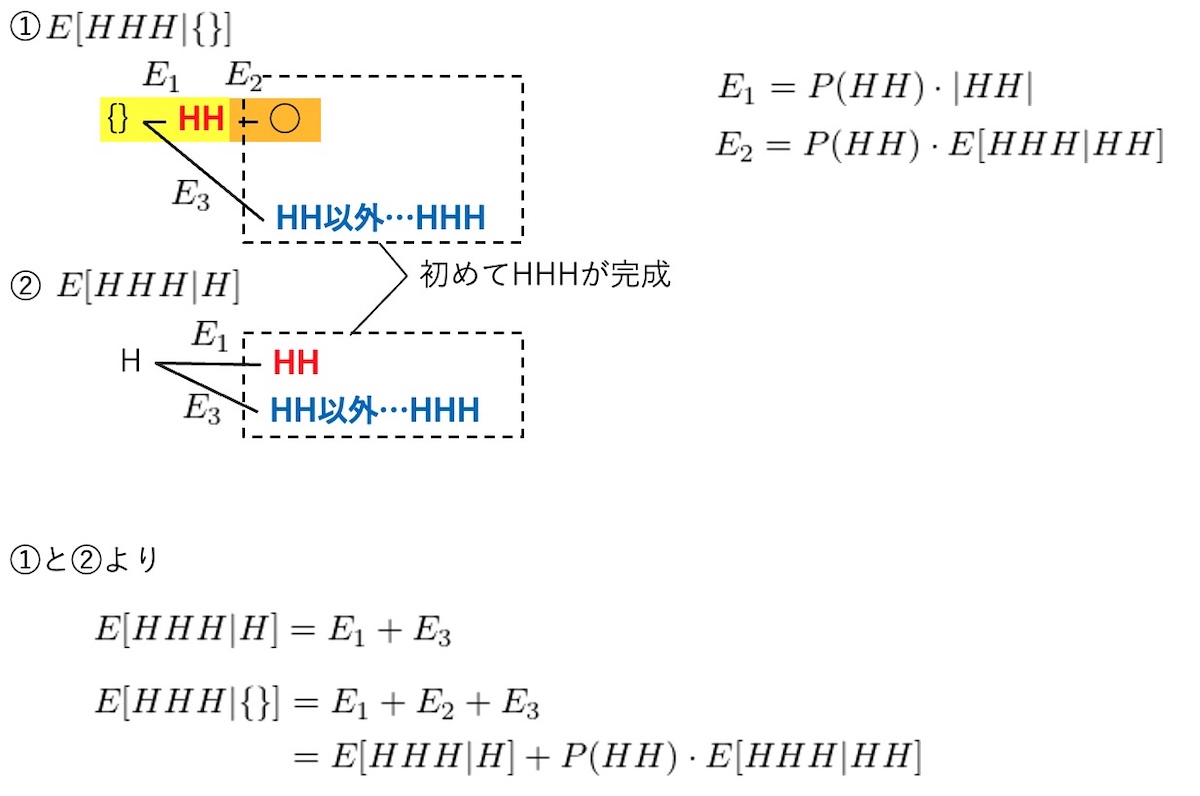
「コインを1度も投げていない状態から」HHHが現れるまでの回数の期待値と,期待値2)の差を考える.
期待値2)と全く同様にして
- 初めてHが出た状態では,HHが出るとHHHが完成する
- 「コインを1度も投げていない状態から」初めてHHが出ると,初めてHHが出た状態に移行する
E[HHH | \{\}]
&= E[HHH | H] + P(HH) \cdot E[HHH|HH]
\end{aligned}
以上をまとめると,求める期待値は
& E[HHH | \{\}] \\
&= E[HHH | HH] \\
&\quad + P(H) \cdot E[HHH|HH] \\
&\quad + P(HH) \cdot E[HHH|HH] \\
&= 2^{3} + 2^{3}/2 + 2^{3}/2^{2} \\
&= 14
\end{aligned}
HTH(8回)
THTも同じ.まず,「性質2」から$E[THT|T] = E[THT|HT] = E[THT|THT] = 2^{3} = 8$となる.
また,
- 初めてTが出た状態では,HTが出るとTHTが完成する
- 「コインを1度も投げていない状態から」初めてHTが出ると,初めてTが出た状態に移行する
& E[HTH|\{\}] \\
&= E[HTH|T] + P(HT) \cdot E[HTH|T]
\end{aligned}
以上をまとめると,求める期待値は
& E[HTH|\{\}] \\
&= E[HTH|T] + P(HT) \cdot E[HTH|T] \\
&= 2^{3} + 2^{3}/2^{2} \\
&= 10
\end{aligned}
HHT, HTT, THH, TTH(8回)
「性質2」から,$2^{3} = 8$回とわかる.注:上記いずれのパターン$X$についても,$E[X|\{\}] = E[X| X\text{のラスト1文字 or 2文字}]$であるため.
まとめ
本記事では,コイントスで特定のパターンが初めて出るまでの回数(期待値)を具体的に計算した.一見不思議な結果も,「HHH」など連続するパターンの完成にはより厳しい条件があるため,期待値が大きくなると理解できる.
| 平均回数(期待値) | パターン |
|---|---|
| 14回 | HHH, TTT |
| 10回 | HTH, THT |
| 8回 | HHT, HTT, THH, TTH |
このような問題をさらに深く理解したい場合は,以下の2つの記事もご覧ください.
マルコフ連鎖を使った計算方法:
➡ コイントスとマルコフ連鎖|長さ3のパターンが出るまでの期待値を計算
条件付き期待値を使った計算方法:
➡ スリーヒットダイス | 条件付き期待値による計算法
