トップ > 数学 > 【統計的仮説検定】手順と例を1ページにまとめる

【統計的仮説検定】手順と例を1ページにまとめる

数学 数学-確率・統計

POINT

  • 統計的仮説検定についての最低限の知識をまとめました．
  • 具体例として，「コイントス」，「母平均についての$Z$検定」を考えます．

統計的仮説検定の考え方は，ポイントさえ抑えてしまえば難しくありません．確率分布の図を描けば，簡単に理解できます．

検出力とサンプルサイズについても言及したかったのですが，最小限の知識に内容を絞りたかったためやめておきました．そのうち書きたいなぁと思っています．

【例1】コイントス

まずは，超極端な例でイメージを掴みましょう．

問題

コイントスを行って表の出た回数に応じて賞金がもらえる博打を考えます．但し，胴元は「コインの表・裏は当確率で出る」としています．

このコインを使ってコイントスを「50回」行ったとき，「50回連続して裏」が出ました．このとき「このコインは表が出やすい，イカサマコインである」と考えられますが，これをどう主張したら良いでしょうか．


すぐに思いつくのは，

  • 『「仮に」胴元の言う通り「コインの表・裏は当確率で出る」というのが正しい』とした場合，「50回連続して裏」が出るのはとても低い確率（$1/2^{50} \simeq 8.9\times 10^{-16}$）だ．
  • だから「コインの表・裏は当確率で出る」というのは正しくないと思うのが自然だ！
と主張することです．このように，確率を具体的に計算することで，定量的な主張ができます．

実は，これが「仮説検定」の考え方です．具体的には，

  1. 「コインは表・裏が当確率で出る」という主張を「帰無仮説$H_0$」と呼ぶ．
  2. $H_0$が正しいと仮定した場合に，得られたデータよりも珍しい事象が起きる確率（※）が，予め決めた確率「有意水準$\alpha$」よりも小さいことを示す．
    （※）これが計算できるものであることが重要！今回であれば「コインが50回以上表が出る確率」
  3. したがって， $H_0$は間違っていると考えられる．つまり，$H_0$の逆の主張「$H_1$：コインは表・裏が当確率ではない」が成り立つであろうとする（「$H_{0}$を棄却する」という）
論法です．このとき，有意水準$\alpha$は「上の論法で$H_{0}$を棄却したときに，実は$H_{0}$が正しかった！という間違い（第1種の誤り）を犯す確率」になっています．



二項分布
コイントスの確率分布（$k$：表の出た回数, $P(k)=\dfrac{50!}{k!(50-k)!}\dfrac{1}{2^{50}}$）


・・・と，ここまで理解できれば，以降の話も理解できるはずです．混乱したら，この「コイントス」に立ち返りましょう．

統計的仮説検定の手順と用語

上の例を一般化した「統計的検定の手順」と「用語」について整理します．その際，以下がポイントになります：

ポイント
  • 検定には様々な手法がある．それぞれのケースに対して，唯一絶対の方法はない．
  • 「ある事象$H_0$の起こる確率が低すぎる」ことを示すのが統計的検定の目的．これが示せれば$H_1$（$H_0$を否定できる場合に成り立つ主張）が支持できる．示せなければ何も言えない．
  • 検定では「$H_0$の起こる確率が低すぎる」ことを示せても，「$H_0$が起きない」ことは示せない．つまり，検定結果は事実とは異なる可能性がある．

以上のポイントを抑えつつ，手順と結果について見てみましょう．

統計的検定の手順：

  1. 否定したい主張を決める：これを帰無仮説$H_0$と呼びます．
    • $H_0$を否定することを，帰無仮説$H_0$を棄却するといいます．逆に，肯定することを採択するといいます．
    • 『$H_0$が棄却された場合に成立する主張$H_1$』を，$H_0$の対立仮説と呼びます．つまり，
      $H_0$が棄却される$\quad\Leftrightarrow\quad H_1$が採択される
      ということです．ここで，$H_1$は必ずしも「$H_0$の論理的な「逆」」にはなりません．以下で，棄却域を右側・左側・両側のいずれから選択するかに左右されます（具体例：下で解説する$Z$検定を参照）．
    • $H_0$が棄却できなかった場合，行った検定は「$H_0$が棄却できなかった」以上の主張を生みません．当然，$H_0$を採択することもできません．
  2. 観測値を用いて，検定統計量$T$（確率変数）を計算する．
    • 「$H_0$が真であるときの$T$の確率分布」がわかっているものとします．
  3. $T$の棄却域の種類を右側・左側・両側のいずれかから選択する．
    • 「棄却域の種類」と「$H_0$」から，$H_1$（$H_0$が棄却された場合に成立する主張）が定まります（具体例：下で解説する$Z$検定を参照）．
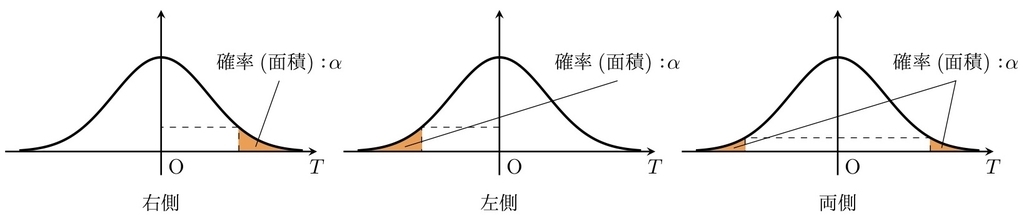
    棄却域の種類
    棄却域の種類
  4. $T$の棄却域の大きさを決定する：つまり『「観測値から計算した$T$の値」を取る確率が$\alpha$以下なら$H_0$が棄却できる』とします．$\alpha$を検定の有意水準と呼びます．
    • 通常$\alpha$は1~10%で設定されます．
  5. 観測値から計算した$T$の値が，確率分布のどこにあるかを調べる．
    • $H_0$は棄却できるのか，できないのか．
    • $H_0$が棄却できた場合は，ギリギリ棄却できたのか，十分に余裕を持って棄却できたのかを調べます．余裕がある場合は，有意水準$\alpha$がもっと小さくても$H_0$を棄却できます．

統計的仮説検定で起こり得る全てのパターン：
全てのパターンは下表で表すことができます．特に，検定結果は事実とは異なる可能性があることに注意しましょう．

表1：検定で起こり得るパターンとその確率
実際の状況（検定者にはわからない）
$H_0$が真$H_1$が真
（$\Rightarrow H_0$が偽．注1）
検定の
結果		$H_0$が棄却されない
（$\Leftrightarrow T$が棄却域にない）
（$\Leftrightarrow $この検定からは何も言えない）		正しい
（確率：$1-\alpha$）		第2種の誤り
（確率：$\beta$）
$H_0$が棄却される
（$\Leftrightarrow T$が棄却域にある）
（$\Leftrightarrow H_1$が採択される）		第1種の誤り
（確率：$\alpha$）		正しい
（確率（検出力）：
$1-\beta$）

注1：この逆（$H_0$が偽$\Rightarrow H_1$が真）は言えません．例えば，後で解説する$Z$検定において棄却域を「右側」とした場合，

  • $H_0$：$\mathrm{E}[\bar{X}]=\mu_0$
  • $H_1$：$\mathrm{E}[\bar{X}]>\mu_0$

です．$\mathrm{E}[\bar{X}]\neq \mu_0$だからといって$\mathrm{E}[\bar{X}]>\mu_0$とは限りません．

【例2】母平均についての$Z$検定

ある母集団（平均：$\mu_0$，分散：$\sigma^2$）から$n$個のサンプルを取り出すことを考えます．このとき，以下の問題は「母平均についての$Z$検定」を適用することができます．
問題

やりたいこと：
  • 母平均$\mu_0$（母集団の平均）と標本平均$\bar{X}$（取り出したサンプルの平均）の間に有意差があるかを調べる．

この検定を使うことのできる条件：

  1. 母分散$\sigma^2$が既知．
    • 未知である場合は，「$t$検定」と呼ばれる方法が存在します．「いつでも$t$検定で良いのでは？」と思うかもしれませんが，母分散$\sigma^2$がわかっているときは$Z$検定のほうが検出力が高いのです．
  2. 母集団が正規分布に従う．

手順：

  1. $H_0$を「$\mathrm{E}[\bar{X}]=\mu_0$」とする．ここで，$\mathrm{E}[\bar{X}]$は$\bar{X}$の期待値を意味します．
  2. 検定統計量を$\displaystyle Z=\frac{\bar{X}-\mu_0}{\sigma/\sqrt{n}}$とします．「$H_0$：$\mathrm{E}[\bar{X}]=\mu_0$」が真であるとき，$Z$は「標準正規分布$\displaystyle N(0,1)=\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{x^2}{2}\right)$」に従います．
  3. 棄却域を「右側・左側・両側」から選びます．
    • 棄却域が「右側」の場合：$H_1$は「$\mathrm{E}[\bar{X}]>\mu_0$」となります．
    • 棄却域が「左側」の場合：$H_1$は「$\mathrm{E}[\bar{X}]<\mu_0$」となります．
    • 棄却域が「両側」の場合：$H_1$は「$\mathrm{E}[\bar{X}]\neq \mu_0$」となります．
    （注：$H_1$が$H_0$の論理的な逆となっているのは棄却域が「両側」の場合だけです．）
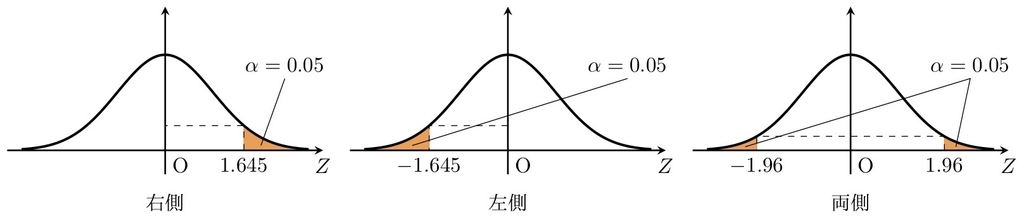
    棄却域の種類
    棄却域の種類（$\alpha=0.05$の場合）
  4. 有意水準$\alpha$を決める（$\alpha=0.05\,(5\%)$とすることが多い）．
  5. サンプルから計算した$Z$が，標準正規分布のどこにあるかを調べる．

参考文献/記事

仮説検定に関する間違いについて参考になる動画です．
www.youtube.com