トップ > プログラミング > PythonでEMアルゴリズム（線形正規モデル・L2正則化）

PythonでEMアルゴリズム（線形正規モデル・L2正則化）

プログラミング プログラミング-Python データ分析 信号処理

書籍「ベイズ信号処理（関原 謙介）」の「第10章　数値実験」の計算例をPythonで実行しました．問題設定やアルゴリズムについては書籍を参照してください．

ベイズ信号処理 ―信号・ノイズ・推定をベイズ的に考える―

ベイズ信号処理 ―信号・ノイズ・推定をベイズ的に考える―

Amazon

出版社のページで正誤表やMATLABコードが公開されています．MATLABコードをそのままPythonにしてもうまくいかず，試行錯誤が必要でした．
ベイズ信号処理 - 共立出版

この記事の続きは以下：
➡Pythonでスパースベイズ - Notes_JP

ライブラリ

import numpy as np
from scipy import linalg
from scipy.linalg import solve_triangular
import matplotlib.pyplot as plt
import matplotlib.cm as cm

結果のプロットに使う関数．

def plot_params(features, memo):
    """
    パラメータの収束をプロット
    """
    if memo['xbar'].shape[0] > 1:
        # パラメータ
        num = len(memo)-1
        fig = plt.figure(figsize=(6.4, 4.8*num/2), tight_layout=True)
        axes = [fig.add_subplot(num, 1, i + 1) for i in range(num)]
        for i, k in enumerate(memo):
            if k == 'xbar': continue
            y = memo[k]
            x = list(range(len(y)))
            axes[i].plot(x, y)
            axes[i].set_xlabel('step')
            if y.ndim == 2:
                axes[i].set_title(f'{k}')
            else:
                axes[i].set_title(f'{k}\n({y[0]:.2e} -> {y[-1]:.2e})')
        plt.show()

        # xbarの変化
        xbars = memo['xbar']
        num = 1
        fig = plt.figure(figsize=(6.4, 4.8*num/2), tight_layout=True)
        axes = [fig.add_subplot(num, 1, i + 1) for i in range(num)]
        for i in range(xbars.shape[0]):
            axes[0].plot(features, xbars[i, :]/xbars[i, :].max(),
                         c=cm.bwr(i/(xbars.shape[0]+1)))
        axes[0].set_ylabel('$y$/max($y$)')
        for ax in axes:
            ax.set_xlabel('$x$')
        plt.show()

    # 最終的なxbar
    xbar = memo['xbar'][-1, :]
    num = 1
    fig = plt.figure(figsize=(6.4, 4.8*num/2), tight_layout=True)
    axes = [fig.add_subplot(num, 1, i + 1) for i in range(num)]
    axes[0].plot(features, xbar/xbar.max())
    for ax in axes:
        ax.set_xlabel('$x$')
        ax.set_ylabel('$y$/max($y$)')
    plt.show()
    return

逆行列の計算に使う関数．numpy.linalg.invを使わない理由は記事末尾のメモを参照．

def inv_cholesky(A):
    """
    正定値実対称行列の逆行列をコレスキー分解を使って計算する
    """
    # Lower-triangular Cholesky factor, A = L * L.T
    L = np.linalg.cholesky(A)  
    invL = solve_triangular(L, np.identity(A.shape[0]), lower=True)
    return invL.T @ invL

データ生成

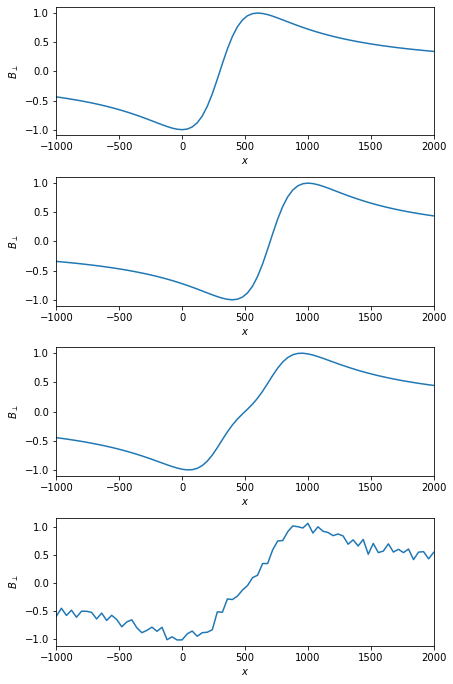
# パラメータ
SNR = 10
d = 300
xmin, xmax = -1000, 2000
X = np.arange(xmin, xmax+1, 40)

# 磁場の計算
def calc_B_perp(X, x0, d):
    """
    B_perp = sin(phi)/r
    """
    r2 = (X-x0)**2+d**2
    return (X-x0)/r2

voxel = np.arange(xmin, xmax+1, 10)
H = np.array([calc_B_perp(x, voxel, d) for x in X])

B_perp_300 = calc_B_perp(X, 300, d)
B_perp_700 = calc_B_perp(X, 700, d)
B_perp_all = B_perp_300 + B_perp_700
B_perp_300 /= np.max(B_perp_300)
B_perp_700 /= np.max(B_perp_700)
B_perp_all /= np.max(B_perp_all)

# ノイズ
Noise = np.random.normal(loc=0.0, scale=1, size=len(X))
Noise *= np.linalg.norm(B_perp_all)/np.linalg.norm(Noise)  # SNR=1
Noise *= 1/SNR
y = B_perp_all + Noise

# データのプロット
num = 4
fig = plt.figure(figsize = (6.4, 4.8 * num / 2), tight_layout = True)
axes = [fig.add_subplot(num, 1, i + 1) for i in range(num)]
axes[0].plot(X, B_perp_300)
axes[1].plot(X, B_perp_700)
axes[2].plot(X, B_perp_all)
axes[3].plot(X, y)
for ax in axes:
    ax.set_xlim(xmin, xmax)
    ax.set_xlabel('$x$')
    ax.set_ylabel('$B_{\perp}$')
plt.show()

ミニマムノルム解（EMアルゴリズム）

ミニマムノルム解を計算する関数．

def L2_EM(nloop, y, H, gamma=0):
    """
    y = Hx
    H: (n_samples, n_features)
    nloop > 0 ならEMアルゴリズムで更新.
    gamma: gammaの初期値. 0なら正則化なし.
    """
    y = y.reshape(-1, 1)
    HT_H = H.T @ H
    HT_y = H.T @ y
    ns, nf = H.shape
    xbar = np.linalg.solve(HT_H + gamma*np.identity(nf), HT_y)
    resid = y - H @ xbar
    beta = ns/((resid.T @ resid).item())
    #
    memo = {
        'alpha':np.empty(nloop+1),
        'beta':np.empty(nloop+1),
        'gamma':np.empty(nloop+1),
        'xbar':np.empty((nloop+1, nf)),
    }
    memo['alpha'][0] = gamma*beta
    memo['beta'][0] = beta
    memo['gamma'][0] = gamma
    memo['xbar'][0, :] = xbar.flatten()
    for i in range(nloop):
        # E step (事後分布 p(x|y)= N(x|xbar, Gamma^{-1})): (4.26)
        Gamma_per_beta = HT_H + gamma*np.identity(nf)
        xbar = np.linalg.solve(Gamma_per_beta, HT_y)
        # M step: (4.29), (4.33)
        invGamma = inv_cholesky(Gamma_per_beta)/beta
        alpha = nf / ((xbar.T @ xbar).item() + np.trace(invGamma))
        resid = y - H @ xbar
        beta = ns/((resid.T @ resid).item() + np.trace(invGamma @ HT_H))
        gamma = alpha/beta
        # memo
        memo['alpha'][i+1] = alpha
        memo['beta'][i+1] = beta
        memo['gamma'][i+1] = gamma
        memo['xbar'][i+1, :] = xbar.flatten()
    return memo

EMアルゴリズムなしのミニマムノルム解：

\begin{aligned}
\bar{\bm{x}}
&= H^{T} (HH^{T} + \gamma I)^{-1} \bm{y} \\
&= (H^{T}H + \gamma I)^{-1} H^{T} \bm{y}
\end{aligned}

lambda_max = np.max(linalg.eigvalsh(H.T @ H))

memo = L2_EM(nloop=0, y=y, H=H, gamma=0)
plot_params(features=voxel, memo=memo)

memo = L2_EM(nloop=0, y=y, H=H, gamma=lambda_max*1e-4)
plot_params(features=voxel, memo=memo)

memo = L2_EM(nloop=0, y=y, H=H, gamma=lambda_max*1e-3)
plot_params(features=voxel, memo=memo)

memo = L2_EM(nloop=0, y=y, H=H, gamma=lambda_max*1e-2)
plot_params(features=voxel, memo=memo)




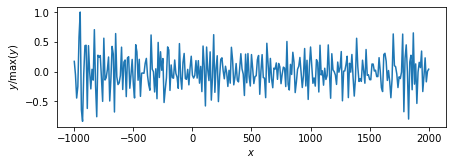
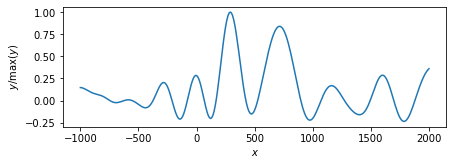
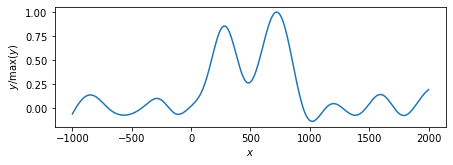
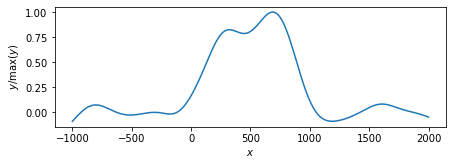
EMアルゴリズムを使って計算した，ベイズ$L_{2}$正則化ミニマムノルム解．

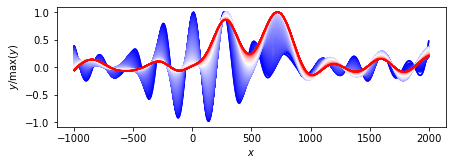
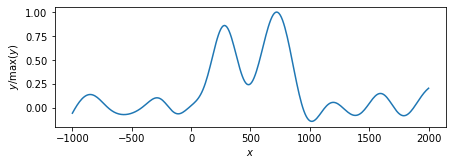
memo = L2_EM(nloop=200, y=y, H=H, gamma=lambda_max*1e-6)
plot_params(features=voxel, memo=memo)

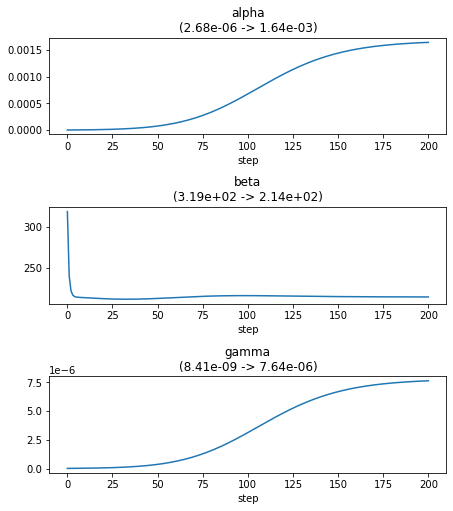
途中経過をすべてプロット．

最終結果のみ．

メモ

(A.51)式
\begin{aligned}
(A^{-1} + B^{T} C^{-1} B)^{-1} B^{T} C^{-1}
= A B^{T} (BAB^{T} + C)^{-1}
\end{aligned}
において，$\gamma$を定数として$A=\gamma^{-1} I$，$C=I$とすると
\begin{aligned}
(\textcolor{red}{B^{T}} B + \gamma I)^{-1} B^{T}
= B^{T} (B\textcolor{red}{B^{T}} + \gamma I)^{-1}
\end{aligned}

これにより，ミニマムノルム解は2通りの表し方ができる．今回は左辺で計算した．

一般論として，逆行列の計算には注意が必要．逆行列×ベクトルの形にしてnp.linalg.solveを使う方が良い．


実対称行列が多く出てくるので，うまい計算法や適したライブラリがあるのかも．

MATLABはこのあたりを自動でうまくやってくれている？