Pythonでスパースベイズ

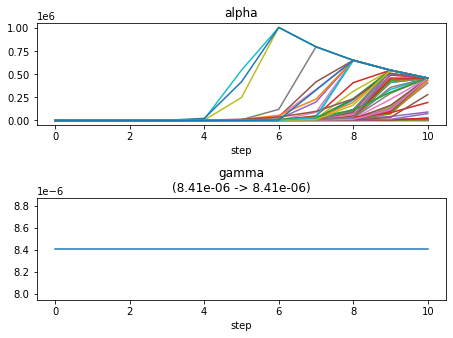
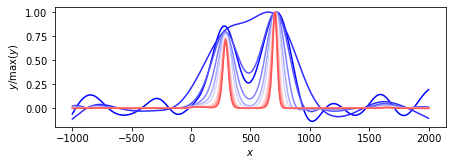
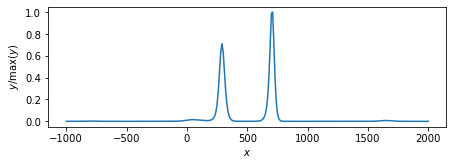
書籍「ベイズ信号処理（関原 謙介）」の「第10章　数値実験」の計算例をPythonで実行しました．問題設定やアルゴリズムについては書籍を参照してください．

ベイズ信号処理 ―信号・ノイズ・推定をベイズ的に考える―

出版社のページで正誤表やMATLABコードが公開されています．MATLABコードをそのままPythonにしてもうまくいかず，試行錯誤が必要でした．
ベイズ信号処理 - 共立出版

以下の記事の続きです．ライブラリ・関数・データはこの記事を参照してください．
➡PythonでEMアルゴリズム（線形正規モデル・L2正則化） - Notes_JP

初期化

def SparseBayes_init(y, H):
    y = y.reshape(-1, 1)
    HT_H = H.T @ H
    HT_y = H.T @ y
    ns, nf = H.shape
    # 正則化ミニマムノルム解からハイパーパラメータalpha(事前分布の精度)の初期値を計算
    lambda_max = np.max(linalg.eigvalsh(HT_H))
    gamma = lambda_max * 1e-3
    xbar = np.linalg.solve(HT_H + gamma*np.identity(nf), HT_y)
    alpha = nf/((xbar.T @ xbar).item())
    alpha_vec = (np.ones(nf) * alpha).reshape(-1,1)
    return xbar, alpha_vec, gamma

更新アルゴリズムごとの関数

EMアルゴリズム．

def SparseBayes_EM(nloop, y, H, beta):
    """
    y = Hx
    H: (n_samples, n_features)
    """
    y = y.reshape(-1, 1)
    HT_H = H.T @ H
    HT_y = H.T @ y
    ns, nf = H.shape
    xbar, alpha_vec, gamma = SparseBayes_init(y=y, H=H)
    #
    memo = {
        'alpha':np.empty((nloop+1, nf)),
        'gamma':np.empty(nloop+1),
        'xbar':np.empty((nloop+1, nf)),
    }
    memo['alpha'][0, :] = alpha_vec.flatten()
    memo['gamma'][0] = gamma
    memo['xbar'][0, :] = xbar.flatten()
    for i in range(nloop):
        Phi = np.diag(alpha_vec.flatten())
        Gamma = Phi + (beta * HT_H)                     # (5.10)
        xbar = beta * np.linalg.solve(Gamma, HT_y)      # (5.11)
        #
        invPhi = (xbar @ xbar.T) + inv_cholesky(Gamma)  # (4.17)
        alpha_vec = 1/np.diag(invPhi)
        # memo
        memo['alpha'][i+1, :] = alpha_vec.flatten()
        memo['gamma'][i+1] = gamma
        memo['xbar'][i+1, :] = xbar.flatten()
    return memo

MacKayのアルゴリズム．

def SparseBayes_MacKay(nloop, y, H, beta):
    """
    y = Hx
    H: (n_samples, n_features)
    """
    y = y.reshape(-1, 1)
    HT_H = H.T @ H
    HT_y = H.T @ y
    ns, nf = H.shape
    xbar, alpha_vec, gamma = SparseBayes_init(y=y, H=H)
    #
    memo = {
        'alpha':np.empty((nloop+1, nf)),
        'gamma':np.empty(nloop+1),
        'xbar':np.empty((nloop+1, nf)),
    }
    memo['alpha'][0, :] = alpha_vec.flatten()
    memo['gamma'][0] = gamma
    memo['xbar'][0, :] = xbar.flatten()
    for i in range(nloop):
        Phi = np.diag(alpha_vec.flatten())
        Gamma = Phi + (beta * HT_H)                     # (5.10)
        xbar = beta * np.linalg.solve(Gamma, HT_y)      # (5.11)
        #
        alpha_vec = beta * np.diag(inv_cholesky(Gamma) @  HT_H) / (xbar.flatten()**2)  # (5.37)
        # 精度が非常に大きく（ボクセル値が非常に小さく）なったボクセルを除外する
        mvv = min(alpha_vec.flatten())
        for j in range(nf):
            alpha_vec[j] = min(alpha_vec[j], 1e10*mvv)
        # memo
        memo['alpha'][i+1, :] = alpha_vec
        memo['gamma'][i+1] = gamma
        memo['xbar'][i+1, :] = xbar.flatten()
    return memo

凸関数の性質に基づくアルゴリズム．

def SparseBayes_convexity(nloop, y, H, beta):
    """
    y = Hx
    H: (n_samples, n_features)
    """
    y = y.reshape(-1, 1)
    HT_H = H.T @ H
    HT_y = H.T @ y
    ns, nf = H.shape
    xbar, alpha_vec, gamma = SparseBayes_init(y=y, H=H)
    #
    memo = {
        'alpha':np.empty((nloop+1, nf)),
        'gamma':np.empty(nloop+1),
        'xbar':np.empty((nloop+1, nf)),
    }
    memo['alpha'][0, :] = alpha_vec.flatten()
    memo['gamma'][0] = gamma
    memo['xbar'][0, :] = xbar.flatten()
    for i in range(nloop):
        Phi = np.diag(alpha_vec.flatten())
        Gamma = Phi + (beta * HT_H)                     # (5.10)
        xbar = beta * np.linalg.solve(Gamma, HT_y)      # (5.11)
        #
        Sigma_y = np.identity(ns)/beta + (H @ np.diag(1/alpha_vec.flatten()) @ H.T) # (5.40)
        z = np.diag(H.T @ inv_cholesky(Sigma_y) @ H)                                # (5.49)
        #
        alpha_vec = np.sqrt(z.flatten())/np.abs(xbar.flatten())                     # (5.53)
        # 精度が非常に大きく（ボクセル値が非常に小さく）なったボクセルを除外する
        mvv = min(alpha_vec.flatten())
        for j in range(nf):
            alpha_vec[j] = min(alpha_vec[j], 1e10*mvv)
        # memo
        memo['alpha'][i+1, :] = alpha_vec
        memo['gamma'][i+1] = gamma
        memo['xbar'][i+1, :] = xbar.flatten()
    return memo

ループ回数：200回

nloop = 200

memo = SparseBayes_EM(nloop=nloop, y=y, H=H, beta=1/np.var(Noise))
plot_params(features=voxel, memo=memo)

memo = SparseBayes_MacKay(nloop=nloop, y=y, H=H, beta=1/np.var(Noise))
plot_params(features=voxel, memo=memo)

memo = SparseBayes_convexity(nloop=nloop, y=y, H=H, beta=1/np.var(Noise))
plot_params(features=voxel, memo=memo)

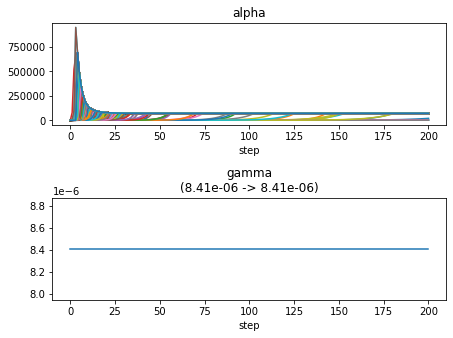
EMアルゴリズム．

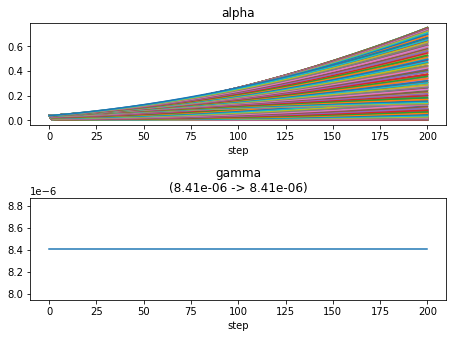
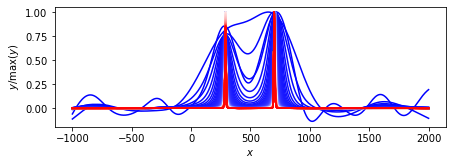
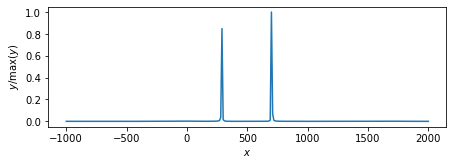
MacKayのアルゴリズム．

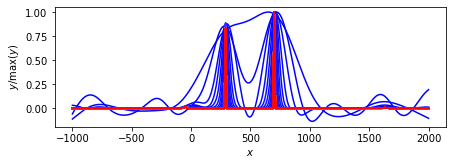
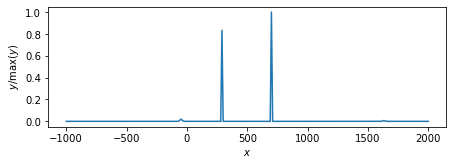
凸関数の性質に基づくアルゴリズム．

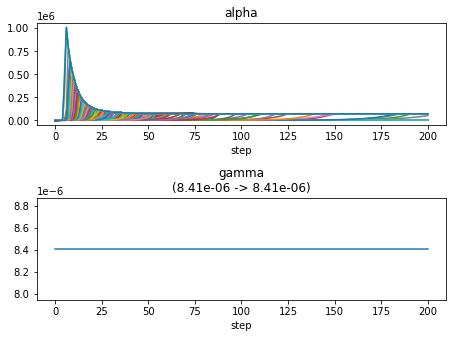
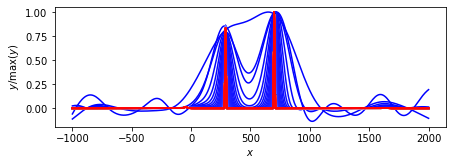
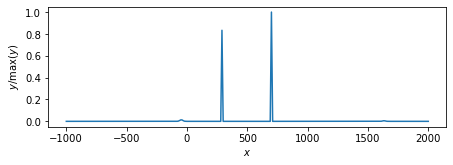
ループ回数：10回

nloop = 10

memo = SparseBayes_EM(nloop=nloop, y=y, H=H, beta=1/np.var(Noise))
plot_params(features=voxel, memo=memo)

memo = SparseBayes_MacKay(nloop=nloop, y=y, H=H, beta=1/np.var(Noise))
plot_params(features=voxel, memo=memo)

memo = SparseBayes_convexity(nloop=nloop, y=y, H=H, beta=1/np.var(Noise))
plot_params(features=voxel, memo=memo)

EMアルゴリズム．

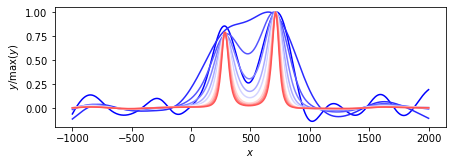
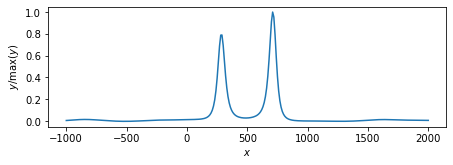
MacKayのアルゴリズム．

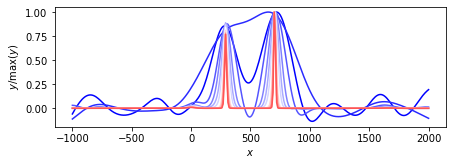
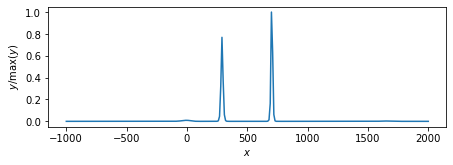
凸関数の性質に基づくアルゴリズム．

文献

• http://signalanalysis.jp/pdfs/SBL_note.pdf