「集合」の上極限・下極限・極限

POINT

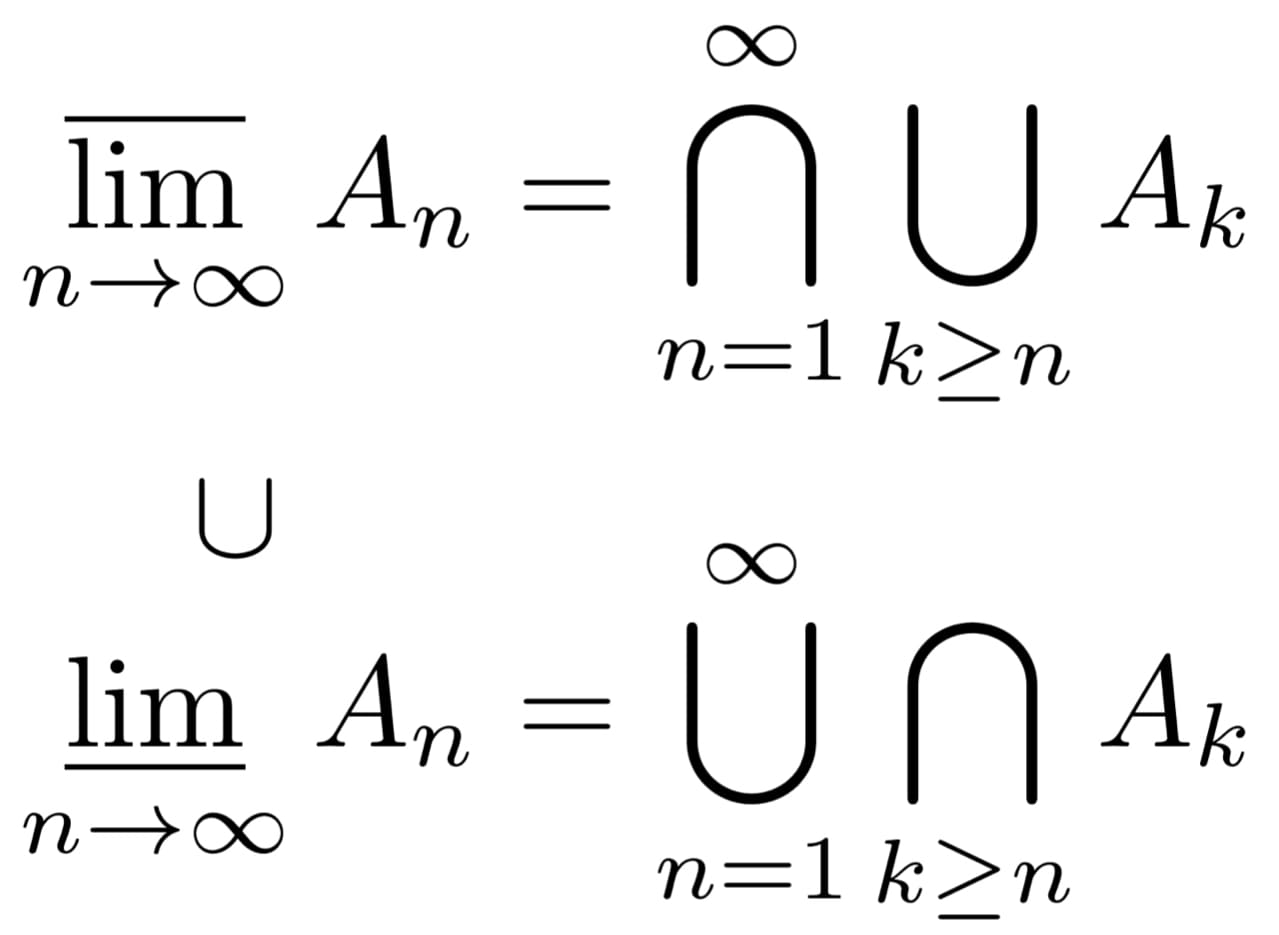
上極限集合，下極限集合を使うための練習．

面倒臭がらずに定義に戻って考えればわかります．証明できるようになると同時に，直感的な意味も把握しておくと性質を思い出しやすいです．
【関連記事】

[A] 「数列」の上極限・下極限・極限 - Notes_JP：数列の上極限・下極限の記事です．

定義
性質
参考文献

定義

集合列$\{A_{n}\}_{n=1}^{\infty}$に対し，上極限集合と下極限集合を次で定義する．

上極限集合

\begin{aligned}
\underset{n\to\infty}{\overline{\lim}} A_{n}
\coloneqq \bigcap_{n=1}^{\infty} \bigcup_{k \geq n} A_{k}
\end{aligned}

下極限集合

\begin{aligned}
\underset{n\to\infty}{\underline{\lim}} A_{n}
\coloneqq \bigcup_{n=1}^{\infty} \bigcap_{k \geq n} A_{k}
\end{aligned}

極限集合

$\underset{n\to\infty}{\overline{\lim}} A_{n} = \underset{n\to\infty}{\underline{\lim}} A_{n}$であるとき，極限集合を

\begin{aligned}
\lim_{n\to\infty} A_{n}
&\coloneqq \underset{n\to\infty}{\overline{\lim}} A_{n} = \underset{n\to\infty}{\underline{\lim}} A_{n}
\end{aligned}

で定める．

上極限集合は，無限個の$A_{n}$に含まれる元からなる（直感的意味）．上の定義を正確に書くと

\begin{aligned}
& x \in \underset{n\to\infty}{\overline{\lim}} A_{n} \\
&\Leftrightarrow \forall n,\: \exists k \geq n \mathrm{\:s.t.\:} x \in A_{k}
\end{aligned}

となる．

下極限集合は，有限個の$A_{n}$を除いたすべての集合に含まれる元からなる（直感的意味）．上の定義を正確に書くと

\begin{aligned}
& x \in \underset{n\to\infty}{\underline{\lim}} A_{n} \\
&\Leftrightarrow \exists n \mathrm{\:s.t.\:} \forall k \geq n,\, x \in A_{k}
\end{aligned}

となる．

性質

包含関係

\begin{aligned}
\underset{n\to\infty}{\underline{\lim}} A_{n}
\subset \underset{n\to\infty}{\overline{\lim}} A_{n}
\end{aligned}

上の「直感的意味」からナイーブにはなりたつことはわかる（「有限個の$A_{n}$を除いたすべての集合に含まれる元」は「無限個の$A_{n}$に含まれる元」である）．ただし，ちゃんと定義に戻って示せるようになることが重要！
【証明】
$x \in \underset{n\to\infty}{\underline{\lim}} A_{n}$とする．下極限集合の定義から，$n_{x}$が存在して$l \geq n_{x} \Rightarrow x \in A_{l}$である．

このとき，任意の$n$に対して$k=\max(n_{x}, n)$とすれば，$k \geq n$かつ$x \in A_{k}$である．したがって，$x\in \underset{n\to\infty}{\overline{\lim}} A_{n}$．//

補集合

\begin{aligned}
& \Bigl(\underset{n\to\infty}{\overline{\lim}} A_{n} \Bigr)^{c}
= \underset{n\to\infty}{\underline{\lim}} (A_{n})^{c} \\
& \Bigl(\underset{n\to\infty}{\underline{\lim}} A_{n} \Bigr)^{c}
= \underset{n\to\infty}{\overline{\lim}} (A_{n})^{c}
\end{aligned}

【証明】
de Morganの公式から

\begin{aligned}
\Bigl(\underset{n\to\infty}{\overline{\lim}} A_{n} \Bigr)^{c}
&= \Biggl( \bigcap_{n=1}^{\infty} \bigcup_{k \geq n} A_{k} \Biggr)^{c} \\
&=\bigcup_{n=1}^{\infty} \Biggl( \bigcup_{k \geq n} A_{k} \Biggr)^{c} \\
&=\bigcup_{n=1}^{\infty} \bigcap_{k \geq n} (A_{k})^{c} \\
&=\underset{n\to\infty}{\underline{\lim}} (A_{n})^{c}
\end{aligned}

となる．

もう一方も同様．あるいは，上の結果で$\{(A_{n})^{c}\}$を考えて，両辺の補集合をとればよい．//

増大列・減少列

$\{A_{n}\}_{n}$が増大列$\Rightarrow \lim A_{n} = \bigcup_{n} A_{n}$
$\{A_{n}\}_{n}$が減少列$\Rightarrow \lim A_{n} = \bigcap_{n} A_{n}$

※メモには解析概論 p.397と書いてある（書籍が手元にない）．

【証明】
1. $\{A_{n}\}$が増大列であるとき，$\bigcup_{k\geq n} A_{k}$は$n$に依らない．これを$A$とすれば，$\overline{\lim} A_{n}=A$．

また，$\bigcap_{k\geq n} A_{k}=A_{n}$であるから，$\underline{\lim} A_{n}=\bigcup_{n} A_{n}=A$．

以上より，$\lim A_{n}=A=\bigcup_{n} A_{n}$．//

2. $\{A_{n}\}$が減少列であるとき， $\{(A_{n})^{c}\}$は増大列である．したがって1. から$\underline{\lim} (A_{n})^{c}=\overline{\lim} (A_{n})^{c}=\bigcup_{n} (A_{n})^{c} = \bigl(\bigcap_{n} A_{n} \bigr)^{c}$が成り立つ．

よって，両辺の補集合を取れば，$\overline{\lim} A_{n}=\underline{\lim} A_{n} = \bigcap_{n} A_{n}$となる．//

（別解）1. と同じ方法でも証明できる．

$\{A_{n}\}$が減少列であるとき，$\bigcap_{k\geq n} A_{k}$は$n$に依らない．これを$A$とすれば，$\underline{\lim} A_{n}=A$．

また，$\bigcup_{k\geq n} A_{k}=A_{n}$であるから，$\overline{\lim} A_{n}=\bigcap_{n} A_{n}=A$．

以上より，$\lim A_{n}=A=\bigcap_{n} A_{n}$．//

その他

その他の関係式

\begin{aligned}
\underset{n\to\infty}{\overline{\lim}} A_{n}
&= \lim_{n\to\infty} \bigcup_{k \geq n} A_{k} \\
\underset{n\to\infty}{\underline{\lim}} A_{n}
&= \lim_{n\to\infty} \bigcap_{k \geq n} A_{k}
\end{aligned}

【証明】
$\{\bigcup_{k \geq n} A_{k}\}_{n}$は減少列なので

\begin{aligned}
\lim_{n\to\infty} \bigcup_{k \geq n} A_{k}
&=\bigcap_{n=1}^{\infty} \bigcup_{k \geq n} A_{k} \\
&=\underset{n\to\infty}{\overline{\lim}} A_{n}
\end{aligned}

となる．

$\{\bigcap_{k \geq n} A_{k}\}_{n}$は増加列なので

\begin{aligned}
\lim_{n\to\infty} \bigcap_{k \geq n} A_{k}
&=\bigcup_{n=1}^{\infty} \bigcap_{k \geq n} A_{k} \\
&=\underset{n\to\infty}{\underline{\lim}} A_{n}
\end{aligned}

となる．//

定義

性質

包含関係

補集合

増大列・減少列

その他

参考文献