音のドップラー効果をガリレイ変換で考える

高校物理では，音のドップラー効果を以下の方法で求めました．
➡【高校物理】ドップラー効果（音波） - Notes_JP

一方，光のドップラー効果は，ローレンツ変換を使って計算されます．この計算と比較するために，音のドップラー効果をガリレイ変換で計算しました．

音のドップラー効果

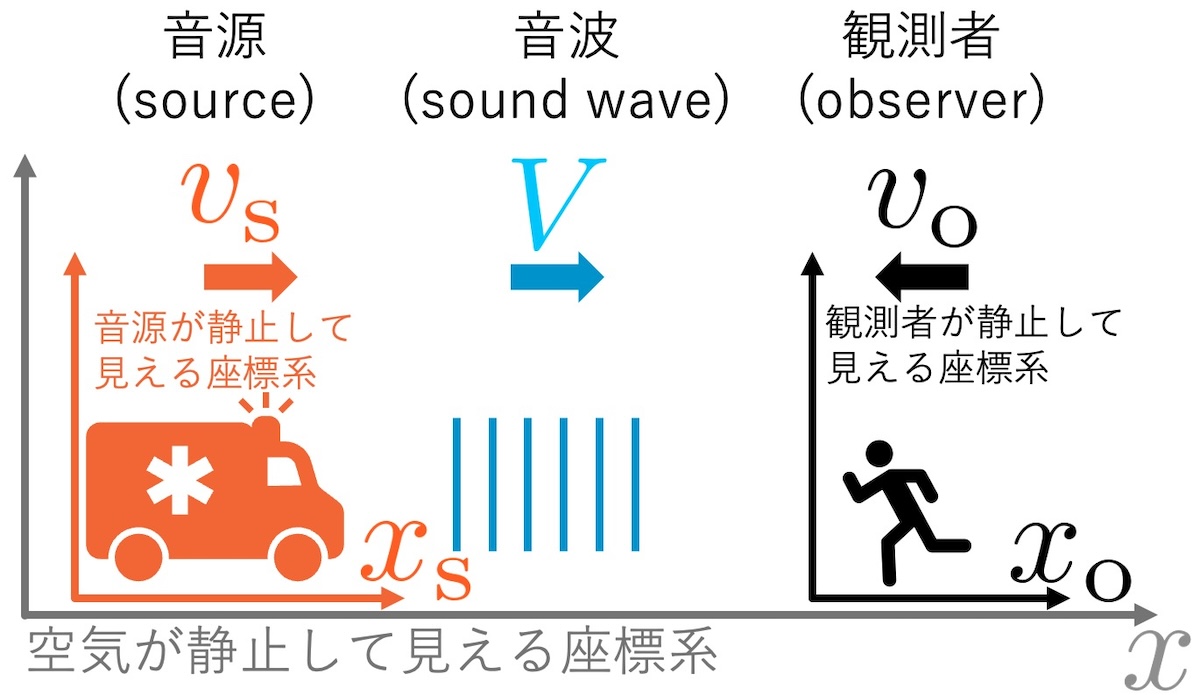
ガリレイ変換による計算

音源が静止してみえる慣性系（座標系）で，音波の位相

\begin{aligned}
k_{\mathrm{s}} x_{\mathrm{s}} - \omega_{\mathrm{s}}t
\end{aligned}

を考えます．これは，

\begin{aligned}
k_{\mathrm{s}} \biggl(x_{\mathrm{s}} - \frac{\omega_{\mathrm{s}}}{k_{\mathrm{s}}} t\biggr)
\end{aligned}

と変形できるため，音源から見た音波の速度は$\dfrac{\omega_{\mathrm{s}}}{k_{\mathrm{s}}}$です．一方で，音源から見た音波の速度は$V - v_{\mathrm{s}}$なので，

\begin{aligned}
\frac{\omega_{\mathrm{s}}}{k_{\mathrm{s}}}
= V - v_{\mathrm{s}}
\end{aligned}

が得られます．

さて，観測者にとっての周波数を得るには，「音源が静止して見える座標系での位相」を「観測者が静止して見える座標系での位相」に変形し，周波数にあたる部分を読み取ればよいです．このときに使う座標変換が「ガリレイ変換」です．

つまり，「ガリレイ変換」は，音源にとっての静止系と，観測者にとっての静止系の間の関係を表したもので，

\begin{aligned}
x_{\mathrm{s}} = x_{\mathrm{o}} - (v_{\mathrm{s}} + v_{\mathrm{o}}) t
\end{aligned}

となります（$t=0$で原点が一致するように選びました）．

観測者が静止してみえる座標系

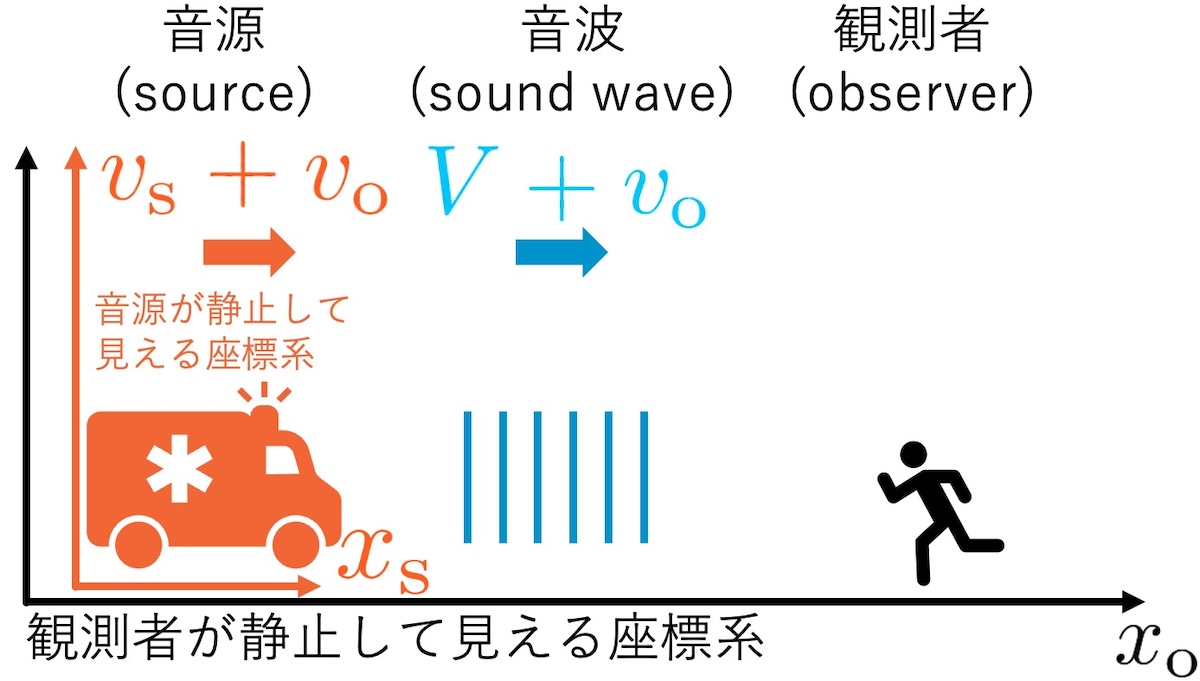
この関係式を使って，音源が静止してみえる慣性系での音波の位相を，観測者が静止して見える座標系で表すと

\begin{aligned}
& k_{\mathrm{s}} x_{\mathrm{s}} - \omega_{\mathrm{s}}t \\
&= k_{\mathrm{s}} \bigl[ x_{\mathrm{o}} - (v_{\mathrm{s}} + v_{\mathrm{o}}) t \bigr] - \omega_{\mathrm{s}}t \\
&= k_{\mathrm{s}}x_{\mathrm{o}} - \biggl[ 1+ \frac{k_{\mathrm{s}}}{\omega_{\mathrm{s}}}(v_{\mathrm{s}} + v_{\mathrm{o}}) \biggr] \omega_{\mathrm{s}} t \\
&= k_{\mathrm{s}}x_{\mathrm{o}} - \frac{V + v_{\mathrm{o}}}{V - v_{\mathrm{s}}} \omega_{\mathrm{s}} t
\end{aligned}

となります．これが観測者が静止して見える座標系からみた位相$k_{\mathrm{o}} x_{\mathrm{o}} - \omega_{\mathrm{o}}t$に等しくなるため，

\begin{aligned}
k_{\mathrm{o}} &= k_{\mathrm{s}} \\
\omega_{\mathrm{o}} &= \frac{V + v_{\mathrm{o}}}{V - v_{\mathrm{s}}} \omega_{\mathrm{s}}
\end{aligned}

がわかります．

$\omega = 2\pi f$と，角周波数を周波数に変換すれば，よく知られた音波のドップラー効果の式

\begin{aligned}
f_{\mathrm{o}} = \frac{V + v_{\mathrm{o}}}{V - v_{\mathrm{s}}} f_{\mathrm{s}}
\end{aligned}

が得られます．

波数（波長）の変換性を利用した計算

上で見たように，音源から見ても観測者からみても波数は同じです（$k_{\mathrm{o}} = k_{\mathrm{s}}$）．どちらから見ても音波の波長が変わらないため，波数$k = 2\pi/\lambda$も変わらないのです．

波数が変わらないこと（$k_{\mathrm{o}} = k_{\mathrm{s}}$）を利用すると，さらに簡単に計算できます．音源の静止系での音速と，観測者の静止系での音速は，それぞれ

\begin{aligned}
\frac{\omega_{\mathrm{s}}}{k_{\mathrm{s}}}
&= V - v_{\mathrm{s}} \\
\frac{\omega_{\mathrm{o}}}{k_{\mathrm{o}}}
&= V + v_{\mathrm{o}}
\end{aligned}

です．これと，$k_{\mathrm{o}} = k_{\mathrm{s}}$から，先ほどと同じ式

\begin{aligned}
\omega_{\mathrm{o}} &= \frac{V + v_{\mathrm{o}}}{V - v_{\mathrm{s}}} \omega_{\mathrm{s}}
\end{aligned}

が得られます．

光のドップラー効果

光のドップラー効果は，ローレンツ変換を使って求めることができます．
➡光のドップラー効果 - Notes_JP