POINT
【関連記事】
- FFTと手計算したフーリエ変換を比較する方法について.
- $T_{\mathrm{s}}$をサンプリング周期とするとき,手計算と比較すべきは「FFTの結果×$T_{\mathrm{s}}$」と「IFFTの結果 / $T_{\mathrm{s}}$」である.
- numpy.fftを使って,ガウス関数のFFTと手計算の比較を行う.
FFT
FFTの場合,手計算の結果を比較すべきは「FFTの結果×$T_{\mathrm{s}}$」である.【理由】
関連記事[A]より,アナログ信号$g(t)$をサンプリング周期$T_{\mathrm{s}}$で「無限個」サンプリングしたデータ列$\{g(k T_{\mathrm{s}})\}_{k=-\infty}^{\infty}$をサンプリングデータを基につくった「連続」信号
\begin{aligned}
g_{\mathrm{s}} (t)
&= \sum_{k=-\infty}^{\infty} g(k T_{\mathrm{s}}) \delta(t - kT_{\mathrm{s}}) \\
&=g(t) \sum_{k=-\infty}^{\infty} \delta(t - kT_{\mathrm{s}})
\end{aligned}
のフーリエ変換はg_{\mathrm{s}} (t)
&= \sum_{k=-\infty}^{\infty} g(k T_{\mathrm{s}}) \delta(t - kT_{\mathrm{s}}) \\
&=g(t) \sum_{k=-\infty}^{\infty} \delta(t - kT_{\mathrm{s}})
\end{aligned}
\begin{aligned}
& G_{\mathrm{s}} (f) = \mathcal{F}[g_{\mathrm{s}}] (f) \\
&= \sum_{k=-\infty}^{\infty} g(k T_{\mathrm{s}}) e^{-i 2\pi f k T_{\mathrm{s}}}\\
&= \frac{1}{T_{\mathrm{s}}} \sum_{n=-\infty}^{\infty} G (f - n f_{\mathrm{s}} ) \tag{1}
\end{aligned}
となる(離散時間フーリエ変換(DTFT)).ここで,$f_{\mathrm{s}} = 1/T_{\mathrm{s}}$はサンプリング周波数,$G=\mathcal{F}[g]$は元の信号$g$のフーリエ変換である.& G_{\mathrm{s}} (f) = \mathcal{F}[g_{\mathrm{s}}] (f) \\
&= \sum_{k=-\infty}^{\infty} g(k T_{\mathrm{s}}) e^{-i 2\pi f k T_{\mathrm{s}}}\\
&= \frac{1}{T_{\mathrm{s}}} \sum_{n=-\infty}^{\infty} G (f - n f_{\mathrm{s}} ) \tag{1}
\end{aligned}
現実の信号を扱う際には,$g_{\mathrm{s}}(t)$に窓関数$w(t)$をかけた$h_{\mathrm{s}}(t) = w(t)g_{\mathrm{s}}(t)$を調べることになる.つまり,
\begin{aligned}
& H_{\mathrm{s}} (f) = \mathcal{F}[h_{\mathrm{s}}] (f) \\
&= \mathcal{F}[w](f)\otimes G_{\mathrm{s}} (f) \tag{2}
\end{aligned}
が計算対象となる.これは,離散フーリエ変換(DFT)& H_{\mathrm{s}} (f) = \mathcal{F}[h_{\mathrm{s}}] (f) \\
&= \mathcal{F}[w](f)\otimes G_{\mathrm{s}} (f) \tag{2}
\end{aligned}
\begin{aligned}
H_{\mathrm{s}} (n f_{\mathrm{s}} / N) = \sum_{k=0}^{N - 1} g(k T_{\mathrm{s}}) e^{-i 2\pi n k / N} \\
(n = 0,...,N-1)
\end{aligned}
をFFTのアルゴリズムで計算することで求める.H_{\mathrm{s}} (n f_{\mathrm{s}} / N) = \sum_{k=0}^{N - 1} g(k T_{\mathrm{s}}) e^{-i 2\pi n k / N} \\
(n = 0,...,N-1)
\end{aligned}
窓関数の影響が無視できるとすれば,式(2)からFFTにより$G_{\mathrm{s}} (f)$が得られる.一方で,手計算で得られるのは$G(f)$であるが,これは式(1)より$G_{\mathrm{s}} (f)$に$T_{\mathrm{s}}$を乗じたものとして得られる.//
IFFT
上の考察から,逆に,$G(f)$をサンプリングしてIFFTすると$g_{\mathrm{s}} (t)\times T_{\mathrm{s}}$が得られることになる.$G(f)$と比較すべきは$g_{\mathrm{s}} (t)$であるから,IFFTの結果を$T_{\mathrm{s}}$で割れば良い.例:ガウス関数
ガウス積分(ガウス積分と派生公式 - Notes_JP)により,\begin{aligned}
&\mathcal{F}[ e^{-(t/\tau)^{2}} ](f)
= \int_{-\infty}^{\infty} e^{-(t/\tau)^{2}} e^{-i2\pi ft} \,\mathrm{d}t \\
&= \tau\sqrt{\pi} e^{-\pi^{2}\tau^{2}f^{2}}
\end{aligned}
であり,逆変換は&\mathcal{F}[ e^{-(t/\tau)^{2}} ](f)
= \int_{-\infty}^{\infty} e^{-(t/\tau)^{2}} e^{-i2\pi ft} \,\mathrm{d}t \\
&= \tau\sqrt{\pi} e^{-\pi^{2}\tau^{2}f^{2}}
\end{aligned}
\begin{aligned}
&\mathcal{F}^{-1}[\tau\sqrt{\pi} e^{-\pi^{2}\tau^{2}f^{2}}](t)
= \tau\sqrt{\pi} \int_{-\infty}^{\infty} e^{-\pi^{2}\tau^{2}f^{2}} e^{i2\pi ft} \,\mathrm{d}f \\
&= e^{-(t/\tau)^{2}}
\end{aligned}
である.&\mathcal{F}^{-1}[\tau\sqrt{\pi} e^{-\pi^{2}\tau^{2}f^{2}}](t)
= \tau\sqrt{\pi} \int_{-\infty}^{\infty} e^{-\pi^{2}\tau^{2}f^{2}} e^{i2\pi ft} \,\mathrm{d}f \\
&= e^{-(t/\tau)^{2}}
\end{aligned}
サンプリング周期$T_{\mathrm{s}}$で$N$点サンプリングすし,時間$[0, NT_{\mathrm{s}}]$の信号を扱うとする.このままだと端で不連続点を生じるので,ガウシアンのピーク位置を$NT_{\mathrm{s}}/2$に持ってくることにする.
上の結果を$\delta t$シフトさせると,
\begin{aligned}
&\mathcal{F}[ e^{-((t-\delta t)/\tau)^{2}} ](f)
= e^{-i2\pi f\cdot \delta t} \mathcal{F}[ e^{-(t/\tau)^{2}} ](f) \\
&= \tau\sqrt{\pi} e^{-\pi^{2}\tau^{2}f^{2}} \cdot e^{-i2\pi f\cdot \delta t}
\end{aligned}
となる(【参考】フーリエ変換の公式と導出 - Notes_JP).
&\mathcal{F}[ e^{-((t-\delta t)/\tau)^{2}} ](f)
= e^{-i2\pi f\cdot \delta t} \mathcal{F}[ e^{-(t/\tau)^{2}} ](f) \\
&= \tau\sqrt{\pi} e^{-\pi^{2}\tau^{2}f^{2}} \cdot e^{-i2\pi f\cdot \delta t}
\end{aligned}
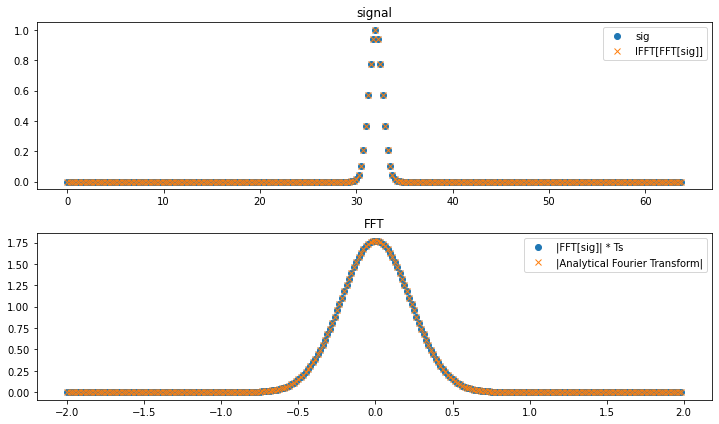
import numpy as np import matplotlib.pyplot as plt def Gauss_t(t, tau, dt): return np.exp(-((t - dt)/tau)**2) def Gauss_f(f, tau, dt): return tau * np.sqrt(np.pi) * np.exp(-(np.pi*tau*f)**2) * np.exp(-1j*2*np.pi*f*dt) # パラメータ定義 Nyquist_freq = 2 # ナイキスト周波数 Ts = 1/(2 * Nyquist_freq) # サンプリング周期 N = 1<<8 # サンプリング点数 t = np.arange(0, N) * Ts # サンプリング時刻 # signal tau = 1 dt = N * Ts / 2 sig = Gauss_t(t, tau, dt) # fft fft = np.fft.fft(sig, n=N) f = np.fft.fftfreq(t.shape[-1], Ts) spectrum_theory = Gauss_f(f, tau, dt) ifft = np.fft.ifft(fft, n=N) # plot num = 2 fig = plt.figure(figsize = (10, 3 * num), tight_layout = True) axes = [fig.add_subplot(num, 1, i + 1) for i in range(num)] axes[0].plot(t, sig, marker='o', ls='None', label='sig') axes[0].plot(t, ifft.real, marker='x', ls='None', label='IFFT[FFT[sig]]') axes[0].set_title('signal') axes[1].plot(f, np.abs(fft)*Ts, marker='o', ls='None', label='|FFT[sig]| * Ts') axes[1].plot(f, np.abs(spectrum_theory), marker='x', ls='None', label='|Analytical Fourier Transform|') axes[1].set_title('FFT') for ax in axes: ax.legend() plt.show()
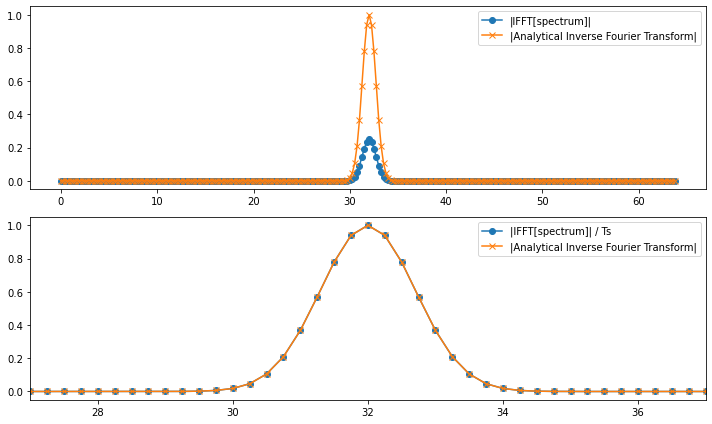
次に,スペクトルを生成して,IFFTと逆フーリエ変換(手計算)を比較する.
# IFFT用の周波数データを定義 f = np.linspace(-Nyquist_freq, Nyquist_freq, N, endpoint=False) # 真ん中を踏むように f = np.concatenate([f[N//2:], f[:N//2]]) spectrum = Gauss_f(f, tau, dt) # 生成データ確認 num = 2 fig = plt.figure(figsize = (10, 3 * num), tight_layout = True) axes = [fig.add_subplot(num, 1, i + 1) for i in range(num)] axes[0].plot(f, marker='o', ls='None') axes[0].set_title('frequency data') axes[1].plot(np.abs(spectrum), marker='o', ls='None') axes[0].set_title('spectrum data') plt.show() # ifft ifft = np.fft.ifft(spectrum, n=N) # plot num = 2 fig = plt.figure(figsize = (10, 3 * num), tight_layout = True) axes = [fig.add_subplot(num, 1, i + 1) for i in range(num)] axes[0].plot(t, np.abs(ifft), marker='o', label='|IFFT[spectrum]|') axes[0].plot(t, sig, marker='x', label='|Analytical Inverse Fourier Transform|') axes[1].plot(t, np.abs(ifft)/Ts, marker='o', label='|IFFT[spectrum]| / Ts') axes[1].plot(t, sig, marker='x', label='|Analytical Inverse Fourier Transform|') axes[1].set_xlim(dt-5, dt+5) for ax in axes: ax.legend() plt.show()