音波（図解）

POINT

• 1次元の音波を図解する．
• 図を書く際は，横軸が「位置」か「時間」かをはっきりさせることが重要．

この記事では，

• $\xi$：流体粒子の平衡位置からの変位．バネで言えば，釣り合い位置からの伸びです．
• $p$：圧力．
• $\displaystyle v=\frac{\partial\xi}{\partial t}$：流体粒子の速度．

とします．

進行波

流体粒子の変位が

\begin{aligned}
\xi(x,t)
&=\sin(kx-\omega t) \\
&=\sin\biggl[k\biggl(x-\frac{\omega}{k}t\biggr)\biggr]
\end{aligned}

で与えられる場合を考えます．このとき，変位の波は$x$軸方向に速度$\omega/k$で伝わっていきます（参考：関数の平行移動と波動 - Notes_JP）．

$t=0$での変位$\xi(x,0)=\sin(kx)$を図示したものが以下です．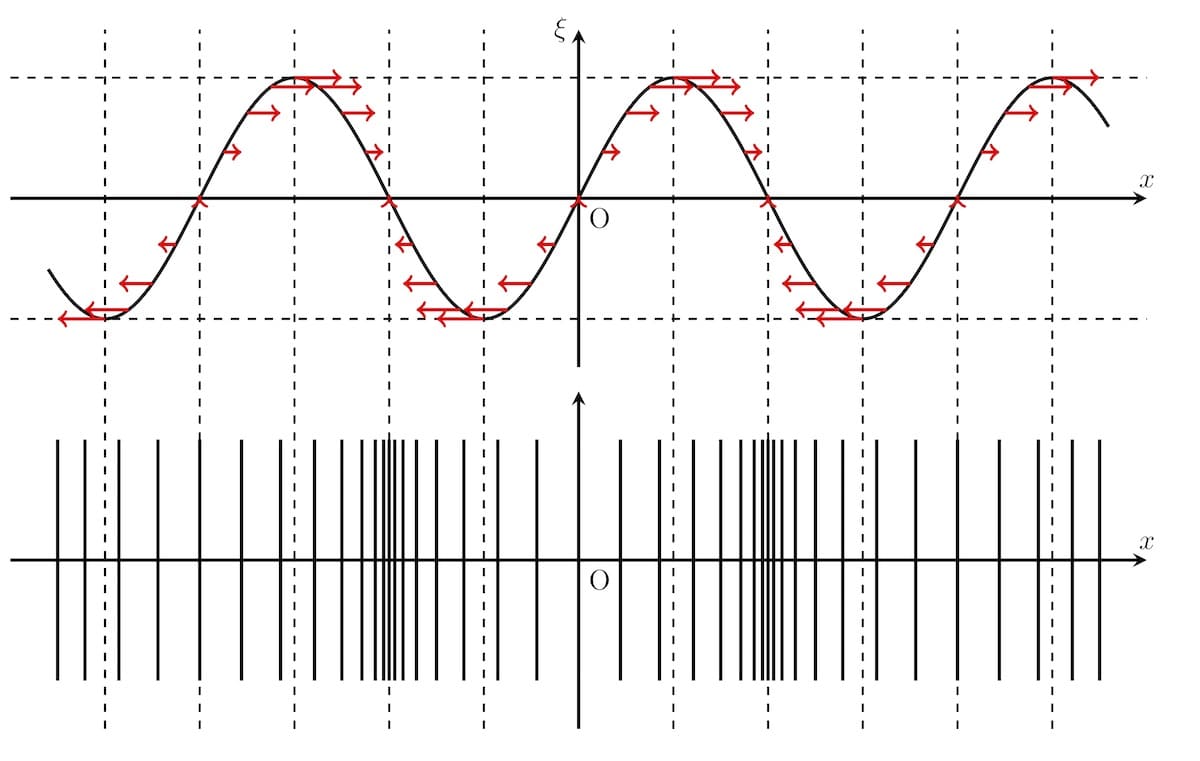

$t=0$での変位

上図の「赤矢印」は，各位置$x$における流体粒子の変位の方向と大きさを表しています．

下図は，「赤矢印」の終点に縦線を引いたものです．これから，

• 流体粒子が集まる「密」の部分．
• 流体粒子が離れる「疎」の部分．

が現れることがわかります．

「密」の部分では圧力が上昇し，「疎」の部分では圧力が減少することから，圧力は下図で表されます．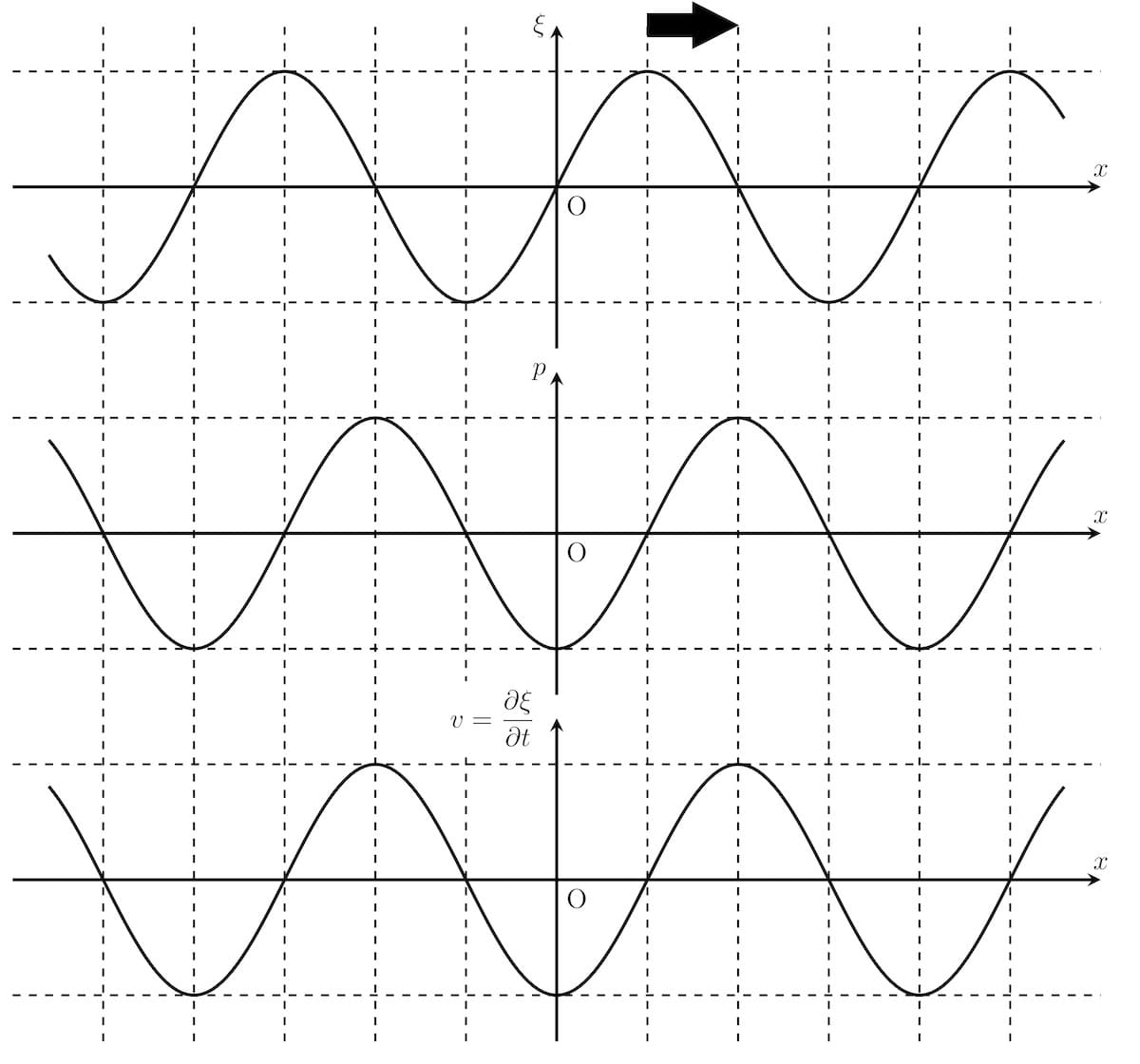

音波の変位$\xi$・圧力$p$・速度$v$．音波の変位，圧力，速度．上図「黒矢印」の方向に波が進行する．

次の関係が成り立っていることに注意しましょう：

変位	最小	ゼロ	最大
圧力	ゼロ	最大 / 最小	ゼロ
速度	ゼロ	最大 / 最小	ゼロ

速度に関しては，

\begin{aligned}
v&=\frac{\partial\xi}{\partial t}
\end{aligned}

から計算できます．$\xi$の図からもわかるように，$\xi(x,t)=\sin(kx-\omega t)$のとき

\begin{aligned}
v&=\frac{\partial\xi}{\partial t} \\
&=-\frac{\omega}{k}\frac{\partial\xi}{\partial x}
\end{aligned}

となることに注意しましょう（$\partial \xi/\partial x$に比例するのではない）．これは，$\xi(x,t)=\sin(kx-\omega t)$を「$kx$を変数として微分する」のと「$-\omega t$を変数として微分する」のが同じであることからわかります．

定在波

そのうち作成．．．

定在波は逆方向に進む進行波の影響があり，上の「進行波」の場合とは異なる振る舞いになります．

コメント

この記事は，音波の速度ポテンシャル（速度ポテンシャル（音波） - Notes_JP）を計算した際，直感的なイメージについて考察したことをまとめたものです．

図はTikZで作成しています．需要があれば公開します．

• TikZ実例集〜2Dグラフ編 - Notes_JP