POINT
- 定義さえ理解しておけば,(派生)公式を覚えなくても計算できる.
- 具体例として,回転体の表面積の派生公式などを導く.
曲面積の定義
まずは,曲面積がどのように定義されるか見てみましょう.パラメータ$\boldsymbol{u}=(u,v)\in\Omega$で定義される曲面
\begin{aligned}
\begin{pmatrix}
x\\
y\\
z
\end{pmatrix}
=
\begin{pmatrix}
X(u,v)\\
Y(u,v)\\
Z(u,v)
\end{pmatrix}
\end{aligned}
の曲面積を求めることを考えます.ここで,\begin{pmatrix}
x\\
y\\
z
\end{pmatrix}
=
\begin{pmatrix}
X(u,v)\\
Y(u,v)\\
Z(u,v)
\end{pmatrix}
\end{aligned}
\begin{aligned}
\boldsymbol{X}(\boldsymbol{u})
=
\begin{pmatrix}
X(u,v)\\
Y(u,v)\\
Z(u,v)
\end{pmatrix}
\end{aligned}
と書くことにします.\boldsymbol{X}(\boldsymbol{u})
=
\begin{pmatrix}
X(u,v)\\
Y(u,v)\\
Z(u,v)
\end{pmatrix}
\end{aligned}
曲面積は,微小な平行四辺形の面積
\begin{aligned}
\frac{\partial \boldsymbol{X}}{\partial u}(\boldsymbol{u})\,\mathrm{d}u
\times
\frac{\partial \boldsymbol{X}}{\partial v}(\boldsymbol{u})\,\mathrm{d}v
\end{aligned}
を足し上げたものとして定義されます:\frac{\partial \boldsymbol{X}}{\partial u}(\boldsymbol{u})\,\mathrm{d}u
\times
\frac{\partial \boldsymbol{X}}{\partial v}(\boldsymbol{u})\,\mathrm{d}v
\end{aligned}
曲面積の定義式
\begin{aligned}
\iint_{\Omega}
\Biggl|
\frac{\partial \boldsymbol{X}}{\partial u}(\boldsymbol{u})
\times
\frac{\partial \boldsymbol{X}}{\partial v}(\boldsymbol{u})
\Biggr|
\,\mathrm{d}u\,\mathrm{d}v
\tag{1}
% \label{eq:surf_area}
\end{aligned}
\iint_{\Omega}
\Biggl|
\frac{\partial \boldsymbol{X}}{\partial u}(\boldsymbol{u})
\times
\frac{\partial \boldsymbol{X}}{\partial v}(\boldsymbol{u})
\Biggr|
\,\mathrm{d}u\,\mathrm{d}v
\tag{1}
% \label{eq:surf_area}
\end{aligned}
【参考】
ここで,
\begin{aligned}
\biggl[
\frac{\partial \boldsymbol{X}}{\partial u}
\times
\frac{\partial \boldsymbol{X}}{\partial v}
\biggr]_i
=\epsilon_{ijk}\partial_u X_j \partial_v X_k
\end{aligned}
であることから,縮約公式を用いて\biggl[
\frac{\partial \boldsymbol{X}}{\partial u}
\times
\frac{\partial \boldsymbol{X}}{\partial v}
\biggr]_i
=\epsilon_{ijk}\partial_u X_j \partial_v X_k
\end{aligned}
\begin{aligned}
&\Biggl|
\frac{\partial \boldsymbol{X}}{\partial u}(\boldsymbol{u})
\times
\frac{\partial \boldsymbol{X}}{\partial v}(\boldsymbol{u})
\Biggr| \\
&=
\sqrt{
\epsilon_{ijk}\partial_u X_j \partial_v X_k\cdot \epsilon_{ilm}\partial_u X_l \partial_v X_m
} \\
&=
\sqrt{
(\partial_u \boldsymbol{X}\cdot \partial_u \boldsymbol{X})(\partial_v \boldsymbol{X}\cdot \partial_v \boldsymbol{X})
-
(\partial_u \boldsymbol{X}\cdot \partial_v \boldsymbol{X})^2
}
\end{aligned}
と表すこともできます.//&\Biggl|
\frac{\partial \boldsymbol{X}}{\partial u}(\boldsymbol{u})
\times
\frac{\partial \boldsymbol{X}}{\partial v}(\boldsymbol{u})
\Biggr| \\
&=
\sqrt{
\epsilon_{ijk}\partial_u X_j \partial_v X_k\cdot \epsilon_{ilm}\partial_u X_l \partial_v X_m
} \\
&=
\sqrt{
(\partial_u \boldsymbol{X}\cdot \partial_u \boldsymbol{X})(\partial_v \boldsymbol{X}\cdot \partial_v \boldsymbol{X})
-
(\partial_u \boldsymbol{X}\cdot \partial_v \boldsymbol{X})^2
}
\end{aligned}
以下「派生公式」で見るように,曲面積の定義式(1)から,よく知られた公式を導くことができます.
派生公式
上の式(1)から,他の公式が簡単に導出されます.球の表面積
定義に従って,「半径$a$の球の表面積:$4\pi a^2$」を導出しましょう.相似比の考え方を用いて,単位球の表面積を$a^2$倍するほうがラクですが,ここでは直接計算してみます.極座標に変数変換します.つまり
\begin{aligned}
\boldsymbol{X}(\theta,\phi)
&=
\begin{pmatrix}
x(\theta,\phi) \\
y(\theta,\phi) \\
z(\theta,\phi)
\end{pmatrix}
=
\begin{pmatrix}
a\sin\theta \cos\phi \\
a\sin\theta \sin\phi \\
a\cos\theta
\end{pmatrix}
\end{aligned}
です.したがって\boldsymbol{X}(\theta,\phi)
&=
\begin{pmatrix}
x(\theta,\phi) \\
y(\theta,\phi) \\
z(\theta,\phi)
\end{pmatrix}
=
\begin{pmatrix}
a\sin\theta \cos\phi \\
a\sin\theta \sin\phi \\
a\cos\theta
\end{pmatrix}
\end{aligned}
\begin{aligned}
&\frac{\partial \boldsymbol{X}}{\partial \theta}
\times
\frac{\partial \boldsymbol{X}}{\partial \phi} \\
=&
\begin{pmatrix}
a\cos\theta \cos\phi \\
a\cos\theta \sin\phi \\
-a\sin\theta
\end{pmatrix}
\times
\begin{pmatrix}
-a\sin\theta \sin\phi \\
a\sin\theta \cos\phi \\
0
\end{pmatrix} \\
=&
\begin{pmatrix}
a^2\sin^2\theta \cos\phi \\
a^2\sin^2\theta \sin\phi \\
a^2\sin\theta \cos\theta
\end{pmatrix}
\end{aligned}
となり,&\frac{\partial \boldsymbol{X}}{\partial \theta}
\times
\frac{\partial \boldsymbol{X}}{\partial \phi} \\
=&
\begin{pmatrix}
a\cos\theta \cos\phi \\
a\cos\theta \sin\phi \\
-a\sin\theta
\end{pmatrix}
\times
\begin{pmatrix}
-a\sin\theta \sin\phi \\
a\sin\theta \cos\phi \\
0
\end{pmatrix} \\
=&
\begin{pmatrix}
a^2\sin^2\theta \cos\phi \\
a^2\sin^2\theta \sin\phi \\
a^2\sin\theta \cos\theta
\end{pmatrix}
\end{aligned}
\begin{aligned}
&
\Biggl|
\frac{\partial \boldsymbol{X}}{\partial \theta}
\times
\frac{\partial \boldsymbol{X}}{\partial \phi}
\Biggr|^2 \\
=&a^4 (\sin^4\theta+\sin^2\theta \cos^2\theta ) \\
=& a^4\sin^2\theta
\end{aligned}
です(最後の等式は$\cos^2=1-\sin^2\theta$を使う).それでは,上半球面を2倍することで計算してみましょう:&
\Biggl|
\frac{\partial \boldsymbol{X}}{\partial \theta}
\times
\frac{\partial \boldsymbol{X}}{\partial \phi}
\Biggr|^2 \\
=&a^4 (\sin^4\theta+\sin^2\theta \cos^2\theta ) \\
=& a^4\sin^2\theta
\end{aligned}
\begin{aligned}
&2
\int\int_{[0,\pi/2]\times [0,2\pi]}
\Biggl|
\frac{\partial \boldsymbol{X}}{\partial \theta}
\times
\frac{\partial \boldsymbol{X}}{\partial \phi}
\Biggr|
\,\mathrm{d}\theta\,\mathrm{d}\phi \\
=&2 \int_0^{2\pi} \,\mathrm{d}\phi\, \int_0^{\pi/2} a^2\sin\theta \,\mathrm{d}\theta \\
=&4\pi a^2\left[-\cos\theta \right]_{0}^{\pi/2} \\
=&4\pi a^2
\end{aligned}
となり,よく知られた公式が導かれました.//&2
\int\int_{[0,\pi/2]\times [0,2\pi]}
\Biggl|
\frac{\partial \boldsymbol{X}}{\partial \theta}
\times
\frac{\partial \boldsymbol{X}}{\partial \phi}
\Biggr|
\,\mathrm{d}\theta\,\mathrm{d}\phi \\
=&2 \int_0^{2\pi} \,\mathrm{d}\phi\, \int_0^{\pi/2} a^2\sin\theta \,\mathrm{d}\theta \\
=&4\pi a^2\left[-\cos\theta \right]_{0}^{\pi/2} \\
=&4\pi a^2
\end{aligned}
グラフの曲面積($X=x$, $Y=y$, $Z=f(x,y)$)
この場合,パラメータは$\boldsymbol{u}=(x,y)$です.$\dfrac{\partial \boldsymbol{X}}{\partial x}\times\dfrac{\partial \boldsymbol{X}}{\partial y}$を計算すると,
\begin{aligned}
\begin{pmatrix}
1\\
0\\
\frac{\partial f}{\partial x}
\end{pmatrix}
\times
\begin{pmatrix}
0\\
1\\
\frac{\partial f}{\partial y}
\end{pmatrix}
=
\begin{pmatrix}
-\frac{\partial f}{\partial x}\\
-\frac{\partial f}{\partial y}\\
1
\end{pmatrix}
\end{aligned}
なので,式(1)を用いると曲面積は\begin{pmatrix}
1\\
0\\
\frac{\partial f}{\partial x}
\end{pmatrix}
\times
\begin{pmatrix}
0\\
1\\
\frac{\partial f}{\partial y}
\end{pmatrix}
=
\begin{pmatrix}
-\frac{\partial f}{\partial x}\\
-\frac{\partial f}{\partial y}\\
1
\end{pmatrix}
\end{aligned}
グラフの曲面積
\begin{aligned}
\iint_{\Omega}
\sqrt{
\left(\frac{\partial f}{\partial x}\right)^2+\left(\frac{\partial f}{\partial y}\right)^2+1
}
\,\mathrm{d}x\,\mathrm{d}y
\end{aligned}
\iint_{\Omega}
\sqrt{
\left(\frac{\partial f}{\partial x}\right)^2+\left(\frac{\partial f}{\partial y}\right)^2+1
}
\,\mathrm{d}x\,\mathrm{d}y
\end{aligned}
$y=f(x)$の回転体($X=x$, $Y=f(x)\cos\theta$, $Z=f(x)\sin\theta$)
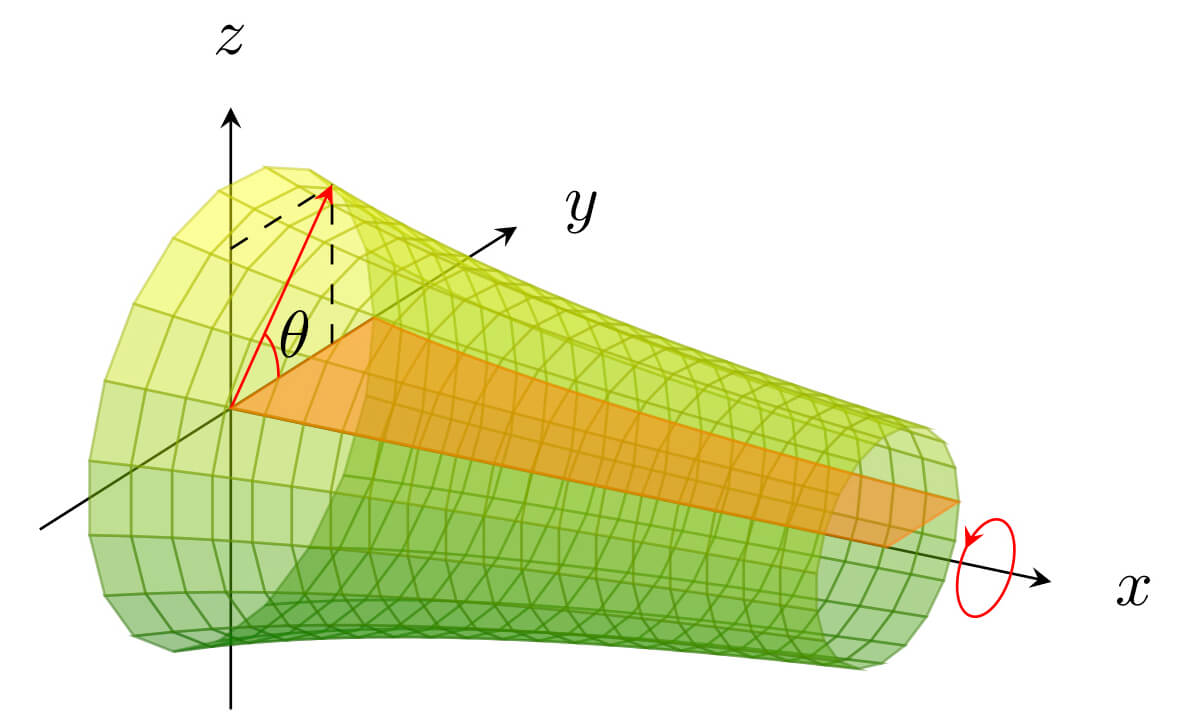
今回は,$\boldsymbol{u}=(x,\theta)$です.
\begin{aligned}
&\dfrac{\partial \boldsymbol{X}}{\partial x}\times\dfrac{\partial \boldsymbol{X}}{\partial \theta} \\
=&
\begin{pmatrix}
1\\
f^\prime(x)\cos\theta\\
f^\prime(x)\sin\theta
\end{pmatrix}
\times
\begin{pmatrix}
0\\
-f(x)\sin\theta\\
f(x)\cos\theta
\end{pmatrix} \\
=&
\begin{pmatrix}
f(x)f^\prime(x)\\
-f(x)\cos\theta\\
-f(x)\sin\theta
\end{pmatrix}
\end{aligned}
なので,式(1)から曲面積は&\dfrac{\partial \boldsymbol{X}}{\partial x}\times\dfrac{\partial \boldsymbol{X}}{\partial \theta} \\
=&
\begin{pmatrix}
1\\
f^\prime(x)\cos\theta\\
f^\prime(x)\sin\theta
\end{pmatrix}
\times
\begin{pmatrix}
0\\
-f(x)\sin\theta\\
f(x)\cos\theta
\end{pmatrix} \\
=&
\begin{pmatrix}
f(x)f^\prime(x)\\
-f(x)\cos\theta\\
-f(x)\sin\theta
\end{pmatrix}
\end{aligned}
\begin{aligned}
\int_0^{2\pi}\,\mathrm{d}\theta\,\int
\sqrt{
\left[f(x)f^\prime(x)\right]^2+f(x)^2
}\,\mathrm{d}x.
\end{aligned}
$\theta$に関する積分を実行すると,おなじみの「回転体の表面積の公式」\int_0^{2\pi}\,\mathrm{d}\theta\,\int
\sqrt{
\left[f(x)f^\prime(x)\right]^2+f(x)^2
}\,\mathrm{d}x.
\end{aligned}
回転体の表面積の公式
\begin{aligned}
2\pi\int
f(x)
\sqrt{
\left[f^\prime(x)\right]^2+1
}
\,\mathrm{d}x
\end{aligned}
2\pi\int
f(x)
\sqrt{
\left[f^\prime(x)\right]^2+1
}
\,\mathrm{d}x
\end{aligned}
回転体の「体積」については以下で解説しています:
【実用例】面積・体積の計算法 - Notes_JP
平面内の曲線$\left( \varphi(t),\psi(t) \right)$の回転体($X=\varphi(t)$, $Y=\psi(t)\cos\theta$, $Z=\psi(t)\sin\theta$)
上の例の一般化です($\varphi(t) = t$, $\psi(t)= f(t)$, $t=x$とすれば,先程の場合になります).これは,$x$-$y$平面の曲線$\left( \varphi(t),\psi(t) \right)$を$x$軸周りに回転させてできた回転体の表面積を求める問題に相当します.
パラメータは$\boldsymbol{u}=(t,\theta)$です.計算方法は上の例とほとんど同じですが,丁寧にやってみましょう:
\begin{aligned}
&\dfrac{\partial \boldsymbol{X}}{\partial t}\times\dfrac{\partial \boldsymbol{X}}{\partial \theta} \\
=&
\begin{pmatrix}
\varphi^\prime(t)\\
\psi^\prime(t)\cos\theta\\
\psi^\prime(t)\sin\theta
\end{pmatrix}
\times
\begin{pmatrix}
0\\
-\psi(t)\sin\theta\\
\psi(t)\cos\theta
\end{pmatrix} \\
=&
\begin{pmatrix}
\psi(t)\psi^\prime(t)\\
-\varphi^\prime(t) \psi(t)\cos\theta\\
-\varphi^\prime(t) \psi(t)\sin\theta
\end{pmatrix}
\end{aligned}
なので,式(1)から曲面積は&\dfrac{\partial \boldsymbol{X}}{\partial t}\times\dfrac{\partial \boldsymbol{X}}{\partial \theta} \\
=&
\begin{pmatrix}
\varphi^\prime(t)\\
\psi^\prime(t)\cos\theta\\
\psi^\prime(t)\sin\theta
\end{pmatrix}
\times
\begin{pmatrix}
0\\
-\psi(t)\sin\theta\\
\psi(t)\cos\theta
\end{pmatrix} \\
=&
\begin{pmatrix}
\psi(t)\psi^\prime(t)\\
-\varphi^\prime(t) \psi(t)\cos\theta\\
-\varphi^\prime(t) \psi(t)\sin\theta
\end{pmatrix}
\end{aligned}
\begin{aligned}
\int_0^{2\pi}\,\mathrm{d}\theta\,\int
\sqrt{
\left[\psi(t)\psi^\prime(t)\right]^2+\varphi^\prime(t)^2\psi(t)^2
}\,\mathrm{d}t.
\end{aligned}
したがって$\theta$に関する積分を実行すると,\int_0^{2\pi}\,\mathrm{d}\theta\,\int
\sqrt{
\left[\psi(t)\psi^\prime(t)\right]^2+\varphi^\prime(t)^2\psi(t)^2
}\,\mathrm{d}t.
\end{aligned}
平面内にある曲線による回転体の表面積
\begin{aligned}
2\pi\int
\psi(t)
\sqrt{
\left[\varphi^\prime(t)\right]^2 + \left[\psi^\prime(t)\right]^2
}
\,\mathrm{d}t
\end{aligned}
2\pi\int
\psi(t)
\sqrt{
\left[\varphi^\prime(t)\right]^2 + \left[\psi^\prime(t)\right]^2
}
\,\mathrm{d}t
\end{aligned}