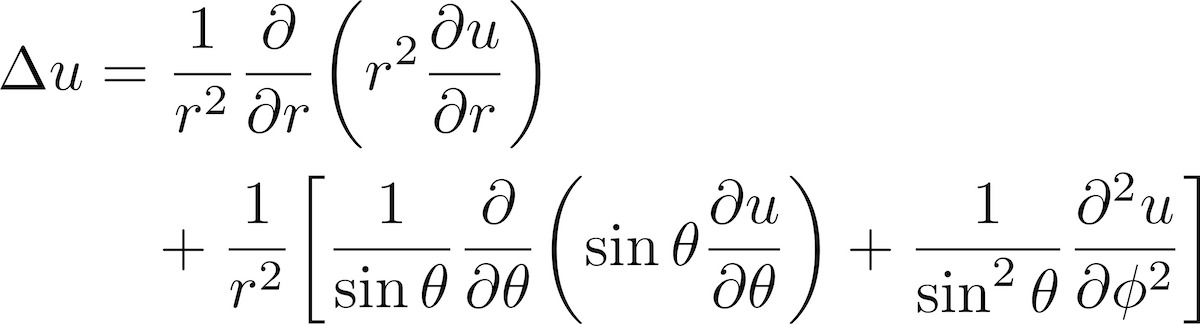
POINT
- 数行でラプラシアン,divを計算する方法(極座標・円筒座標).
- 面倒な偏微分の計算(連鎖率・チェーンルール・合成関数の微分)は不要.
【前提知識】
- 極座標・円筒座標のナブラ(grad)の表式.
- 積分の変数変換の方法(ヤコビアンの計算方法).
- ガウスの発散定理.
関連記事[A]の一般論(曲線座標系)における複雑な議論を徹底的に避けました(計算方法は同じ).極座標・円筒座標についての計算方法だけを知りたい方は,この記事だけを読めば十分です.
【関連記事】
[A]曲線座標系のラプラシアン(一般論)
[B]曲線座標系のナブラの求め方
導出の概要
極座標のラプラシアンを導出する場合を例に導出の概要を説明します.【導出の概要】
$\psi(x,y,z)$を「ある(有限な)領域の外では$0$になるような任意関数」とします.このとき,
\begin{aligned}
&\int \psi \cdot \biggl(\textcolor{red}{
\frac{\partial^2 u}{\partial x^2}
+ \frac{\partial^2 u}{\partial y^2}
+ \frac{\partial^2 u}{\partial z^2}
} \biggr)
\,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z \\
&=\cdots \\
&=\int \psi \cdot (\textcolor{red}{\text{極座標の変数の式}} ) \,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z
\end{aligned}
と変形できれば($\psi$が任意関数であることから)&\int \psi \cdot \biggl(\textcolor{red}{
\frac{\partial^2 u}{\partial x^2}
+ \frac{\partial^2 u}{\partial y^2}
+ \frac{\partial^2 u}{\partial z^2}
} \biggr)
\,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z \\
&=\cdots \\
&=\int \psi \cdot (\textcolor{red}{\text{極座標の変数の式}} ) \,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z
\end{aligned}
\begin{aligned}
&\color{red}{ \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial z^2} } \\
&=(\textcolor{red}{\text{極座標の変数の式}} )
\end{aligned}
であることがわかります.この式は,&\color{red}{ \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial z^2} } \\
&=(\textcolor{red}{\text{極座標の変数の式}} )
\end{aligned}
\begin{aligned}
&(\text{極座標のラプラシアン}) \\
&=(\text{極座標の変数の式})
\end{aligned}
を意味しています.&(\text{極座標のラプラシアン}) \\
&=(\text{極座標の変数の式})
\end{aligned}
極座標
勾配 (grad)
極座標のナブラは\begin{aligned}
\boldsymbol{\nabla}
&= \boldsymbol{e}_r \frac{\partial}{\partial r}
+\boldsymbol{e}_\theta \frac{1}{r}\frac{\partial}{\partial \theta}
+\boldsymbol{e}_\phi \frac{1}{r\sin\theta}\frac{\partial}{\partial \phi}
\end{aligned}
なので,\boldsymbol{\nabla}
&= \boldsymbol{e}_r \frac{\partial}{\partial r}
+\boldsymbol{e}_\theta \frac{1}{r}\frac{\partial}{\partial \theta}
+\boldsymbol{e}_\phi \frac{1}{r\sin\theta}\frac{\partial}{\partial \phi}
\end{aligned}
極座標の勾配 (gradient)
\begin{aligned}
\boldsymbol{\nabla}\psi
= \boldsymbol{e}_r \frac{\partial \psi}{\partial r}
+\boldsymbol{e}_\theta \frac{1}{r}\frac{\partial \psi}{\partial \theta}
+\boldsymbol{e}_\phi \frac{1}{r\sin\theta}\frac{\partial \psi}{\partial \phi}
\end{aligned}
\boldsymbol{\nabla}\psi
= \boldsymbol{e}_r \frac{\partial \psi}{\partial r}
+\boldsymbol{e}_\theta \frac{1}{r}\frac{\partial \psi}{\partial \theta}
+\boldsymbol{e}_\phi \frac{1}{r\sin\theta}\frac{\partial \psi}{\partial \phi}
\end{aligned}
発散 (div)
まずベクトル解析の公式\begin{aligned}
\boldsymbol{\nabla}\cdot ( \psi \boldsymbol{A})
= \boldsymbol{\nabla}\psi \cdot \boldsymbol{A}
+\psi ( \boldsymbol{\nabla}\cdot\boldsymbol{A})
\end{aligned}
から\boldsymbol{\nabla}\cdot ( \psi \boldsymbol{A})
= \boldsymbol{\nabla}\psi \cdot \boldsymbol{A}
+\psi ( \boldsymbol{\nabla}\cdot\boldsymbol{A})
\end{aligned}
\begin{aligned}
&\int \psi (\textcolor{red}{\mathrm{div\,} \boldsymbol{A}} )
\,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z \\
&=\int \psi (\boldsymbol{\nabla}\cdot\boldsymbol{A}) \,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z \\
&=-\int \boldsymbol{\nabla}\psi \cdot \boldsymbol{A} \,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z \\
&\qquad\qquad\qquad
+\underbrace{\int \boldsymbol{\nabla}\cdot ( \psi \boldsymbol{A})
\,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z }_{=0}\\
&=-\int\biggl[\frac{\partial \psi}{\partial r}A_r
+\frac{1}{r}\frac{\partial \psi}{\partial \theta}A_\theta
+\frac{1}{r\sin\theta}\frac{\partial \phi}{\partial \phi}A_\phi
\biggr] \\
&\qquad\qquad\qquad\qquad\qquad\quad
\times r^2\sin\theta\,\mathrm{d}r\,\mathrm{d}\theta\,\mathrm{d}\phi
\end{aligned}
となります.但し,以下の操作を行いました:&\int \psi (\textcolor{red}{\mathrm{div\,} \boldsymbol{A}} )
\,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z \\
&=\int \psi (\boldsymbol{\nabla}\cdot\boldsymbol{A}) \,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z \\
&=-\int \boldsymbol{\nabla}\psi \cdot \boldsymbol{A} \,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z \\
&\qquad\qquad\qquad
+\underbrace{\int \boldsymbol{\nabla}\cdot ( \psi \boldsymbol{A})
\,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z }_{=0}\\
&=-\int\biggl[\frac{\partial \psi}{\partial r}A_r
+\frac{1}{r}\frac{\partial \psi}{\partial \theta}A_\theta
+\frac{1}{r\sin\theta}\frac{\partial \phi}{\partial \phi}A_\phi
\biggr] \\
&\qquad\qquad\qquad\qquad\qquad\quad
\times r^2\sin\theta\,\mathrm{d}r\,\mathrm{d}\theta\,\mathrm{d}\phi
\end{aligned}
- Gaussの発散定理を用いて,表面項を落とした(仮定から,十分大きな曲面$S$を取れば,$S$の上で$\psi=0$となるようできる):\begin{aligned}
\int_V \boldsymbol{\nabla}\cdot ( \psi \boldsymbol{A})\,\mathrm{d}V
=\int_S \psi \boldsymbol{A}\cdot \mathrm{d} \boldsymbol{S}
=0
\end{aligned} - ベクトルの極座標の成分を使った:$\boldsymbol{A}= A_r \boldsymbol{e}_r +A_\theta \boldsymbol{e}_\theta+A_\phi \boldsymbol{e}_\phi$.
- 極座標に変数変換した:$(x,y,z)\rightarrow (r,\theta,\phi)$,$\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z=r^2\sin\theta \,\mathrm{d}r\,\mathrm{d}\theta\,\mathrm{d}\phi$
さらに
- 各項について部分積分を行い,$\psi$から微分を移す
- $x,y,z$に変数変換を行う$\displaystyle \biggl( \,\mathrm{d}r\,\mathrm{d}\theta\,\mathrm{d}\phi=\frac{1}{r^2\sin\theta}\,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z\biggr)$
ことで,次の式に変形できます:
\begin{aligned}
&=\int\psi\textcolor{red}{\biggl[\frac{\partial}{\partial r}(r^2\sin\theta A_r)}\\
&\qquad\qquad \textcolor{red}{
+\frac{\partial}{\partial \theta}(r\sin\theta A_\theta)
+\frac{\partial}{\partial \phi}(r A_\phi)\biggr] }
\frac{\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z}{\textcolor{red}{r^2\sin\theta}}.
\end{aligned}
&=\int\psi\textcolor{red}{\biggl[\frac{\partial}{\partial r}(r^2\sin\theta A_r)}\\
&\qquad\qquad \textcolor{red}{
+\frac{\partial}{\partial \theta}(r\sin\theta A_\theta)
+\frac{\partial}{\partial \phi}(r A_\phi)\biggr] }
\frac{\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z}{\textcolor{red}{r^2\sin\theta}}.
\end{aligned}
ここで$\psi$は任意関数であることから ,赤字同士が等しくなります(詳しく知りたい方は,次を参照してください:【補足】∫(ψ・f)=0(ψは任意関数)⇒f=0となる理由):
極座標の発散 (divergence)
\begin{aligned}
\mathrm{div\,} \boldsymbol{A}
&=\frac{1}{r^2}\frac{\partial}{\partial r}(r^2 A_r)\\
&\qquad
+\frac{1}{r\sin\theta}\frac{\partial}{\partial \theta}(\sin\theta A_\theta)\\
&\qquad
+\frac{1}{r\sin\theta}\frac{\partial A_\phi}{\partial \phi}
\end{aligned}
\mathrm{div\,} \boldsymbol{A}
&=\frac{1}{r^2}\frac{\partial}{\partial r}(r^2 A_r)\\
&\qquad
+\frac{1}{r\sin\theta}\frac{\partial}{\partial \theta}(\sin\theta A_\theta)\\
&\qquad
+\frac{1}{r\sin\theta}\frac{\partial A_\phi}{\partial \phi}
\end{aligned}
ラプラシアン
ラプラシアンは$\Delta u=\mathrm{div\,} (\mathrm{grad\,}u)$です.したがって,発散の計算で$\boldsymbol{A}$を$\mathrm{grad\,}u=\boldsymbol{\nabla}u$に置き換えれば,ラプラシアンを導くことができます.つまり,上で求めた表式に$\displaystyle \; A_r=\frac{\partial u}{\partial r}$,$\displaystyle A_\theta=\frac{1}{r}\frac{\partial u}{\partial \theta}$,$\displaystyle A_\phi=\frac{1}{r\sin\theta}\frac{\partial u}{\partial \phi}\;$を代入すればよく,極座標のラプラシアン (Laplacian)
\begin{aligned}
\Delta u
&= \frac{1}{r^2}\frac{\partial}{\partial r}\biggl(r^2 \frac{\partial u}{\partial r} \biggr) \\
&\quad
+\frac{1}{r^2}\biggl[\frac{1}{\sin\theta}\frac{\partial}{\partial \theta}\biggl(\sin\theta \frac{\partial u}{\partial \theta} \biggr)
+\frac{1}{\sin^2\theta}\frac{\partial^2 u}{\partial \phi^2}
\biggr]
\end{aligned}
\Delta u
&= \frac{1}{r^2}\frac{\partial}{\partial r}\biggl(r^2 \frac{\partial u}{\partial r} \biggr) \\
&\quad
+\frac{1}{r^2}\biggl[\frac{1}{\sin\theta}\frac{\partial}{\partial \theta}\biggl(\sin\theta \frac{\partial u}{\partial \theta} \biggr)
+\frac{1}{\sin^2\theta}\frac{\partial^2 u}{\partial \phi^2}
\biggr]
\end{aligned}
\begin{aligned}
\frac{1}{r^2} \frac{\partial}{\partial r}\biggl(r^2 \frac{\partial u}{\partial r} \biggr)
&=\frac{1}{r^2}\biggl(2r\frac{\partial u}{\partial r} + r^2 \frac{\partial^2 u}{\partial r^2} \biggr) \\
&=\frac{\partial^2 u}{\partial r^2}+\frac{2}{r}\frac{\partial u}{\partial r} \\
&=\frac{1}{r} \frac{\partial^2}{\partial r^2} ( ru )
\end{aligned}
と表すこともできます.最後の表式を使うと,簡単に計算が実行できることがあります(例えば$u\propto 1/r$の場合:ちょっと感動した計算 - Notes_JP).\frac{1}{r^2} \frac{\partial}{\partial r}\biggl(r^2 \frac{\partial u}{\partial r} \biggr)
&=\frac{1}{r^2}\biggl(2r\frac{\partial u}{\partial r} + r^2 \frac{\partial^2 u}{\partial r^2} \biggr) \\
&=\frac{\partial^2 u}{\partial r^2}+\frac{2}{r}\frac{\partial u}{\partial r} \\
&=\frac{1}{r} \frac{\partial^2}{\partial r^2} ( ru )
\end{aligned}
円筒座標
極座標の場合と全く同様の方法で導くことができます.勾配 (grad)
円筒座標のナブラは\begin{aligned}
\boldsymbol{\nabla}
= \boldsymbol{e}_r \frac{\partial}{\partial r}
+\boldsymbol{e}_\theta \frac{1}{r}\frac{\partial}{\partial \theta}
+\boldsymbol{e}_z \frac{\partial}{\partial z}
\end{aligned}
であることから,\boldsymbol{\nabla}
= \boldsymbol{e}_r \frac{\partial}{\partial r}
+\boldsymbol{e}_\theta \frac{1}{r}\frac{\partial}{\partial \theta}
+\boldsymbol{e}_z \frac{\partial}{\partial z}
\end{aligned}
円筒座標の勾配 (gradient)
\begin{aligned}
\boldsymbol{\nabla}\psi
= \boldsymbol{e}_r \frac{\partial \psi}{\partial r}
+\boldsymbol{e}_\theta \frac{1}{r}\frac{\partial \psi}{\partial \theta}
+\boldsymbol{e}_\phi \frac{\partial \psi}{\partial z}
\end{aligned}
\boldsymbol{\nabla}\psi
= \boldsymbol{e}_r \frac{\partial \psi}{\partial r}
+\boldsymbol{e}_\theta \frac{1}{r}\frac{\partial \psi}{\partial \theta}
+\boldsymbol{e}_\phi \frac{\partial \psi}{\partial z}
\end{aligned}
発散 (div)
発散・ラプラシアンも極座標の場合とまったく同様に計算できます.丁寧に見てみましょう.\begin{aligned}
&\int \psi\left(\color{red}{\mathrm{div\,} \boldsymbol{A}} \right) \,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z \\
&=\int \psi\left(\boldsymbol{\nabla}\cdot\boldsymbol{A}\right) \,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z \\
&=-\int \boldsymbol{\nabla}\psi \cdot \boldsymbol{A} \,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z
+\underset{=0}{\underline{\int \boldsymbol{\nabla}\cdot \left( \psi \boldsymbol{A}\right) \,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z }}\\
&=-\int\biggl[ \frac{\partial \psi}{\partial r} A_r
+ \frac{1}{r}\frac{\partial \psi}{\partial \theta} A_\theta
+ \frac{\partial \psi}{\partial z} A_z
\biggr] r\,\mathrm{d}r\,\mathrm{d}\theta\,\mathrm{d}z\\
&=\int \psi \textcolor{red}{\biggl[ \frac{\partial }{\partial r} (r A_r)
+ \frac{\partial A_\theta}{\partial \theta}
+ r \frac{\partial A_z}{\partial z}
\biggr] \frac{1}{r}} \,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z
\end{aligned}
ここで$\psi$は任意関数であることから ,以下が成立します(【補足】∫(ψ・f)=0(ψは任意関数)⇒f=0となる理由):&\int \psi\left(\color{red}{\mathrm{div\,} \boldsymbol{A}} \right) \,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z \\
&=\int \psi\left(\boldsymbol{\nabla}\cdot\boldsymbol{A}\right) \,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z \\
&=-\int \boldsymbol{\nabla}\psi \cdot \boldsymbol{A} \,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z
+\underset{=0}{\underline{\int \boldsymbol{\nabla}\cdot \left( \psi \boldsymbol{A}\right) \,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z }}\\
&=-\int\biggl[ \frac{\partial \psi}{\partial r} A_r
+ \frac{1}{r}\frac{\partial \psi}{\partial \theta} A_\theta
+ \frac{\partial \psi}{\partial z} A_z
\biggr] r\,\mathrm{d}r\,\mathrm{d}\theta\,\mathrm{d}z\\
&=\int \psi \textcolor{red}{\biggl[ \frac{\partial }{\partial r} (r A_r)
+ \frac{\partial A_\theta}{\partial \theta}
+ r \frac{\partial A_z}{\partial z}
\biggr] \frac{1}{r}} \,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z
\end{aligned}
円筒座標の発散 (divergence)
\begin{aligned}
\mathrm{div\,} \boldsymbol{A}
= \frac{1}{r}\frac{\partial}{\partial r} (r A_r)
+\frac{1}{r}\frac{\partial A_\theta}{\partial \theta}
+\frac{\partial A_z}{\partial z}
\end{aligned}
\mathrm{div\,} \boldsymbol{A}
= \frac{1}{r}\frac{\partial}{\partial r} (r A_r)
+\frac{1}{r}\frac{\partial A_\theta}{\partial \theta}
+\frac{\partial A_z}{\partial z}
\end{aligned}
ラプラシアン
発散の計算で$\boldsymbol{A}$を$\boldsymbol{\nabla}u$に置き換えれば,ラプラシアンを導くことができます.つまり,上で求めた表式に$\;\displaystyle A_r=\frac{\partial u}{\partial r}$,$\displaystyle A_\theta=\frac{1}{r}\frac{\partial u}{\partial \theta}$,$\displaystyle A_z=\frac{\partial u}{\partial z}\;$を代入することにより,以下が導かれます:円筒座標のラプラシアン (Laplacian)
\begin{aligned}
\Delta u
= \frac{1}{r}\frac{\partial}{\partial r}\left(r \frac{\partial u}{\partial r} \right)
+\frac{1}{r^2}\frac{\partial^2 u}{\partial \theta^2}
+\frac{\partial^2 u}{\partial z^2}
\end{aligned}
\Delta u
= \frac{1}{r}\frac{\partial}{\partial r}\left(r \frac{\partial u}{\partial r} \right)
+\frac{1}{r^2}\frac{\partial^2 u}{\partial \theta^2}
+\frac{\partial^2 u}{\partial z^2}
\end{aligned}